Hasura – Triggers
Has
Hasura – Deployment
Deploying or Running Hasura on AWS ECS Fargate
Create a Task Definition
- Use the right hasura docker image
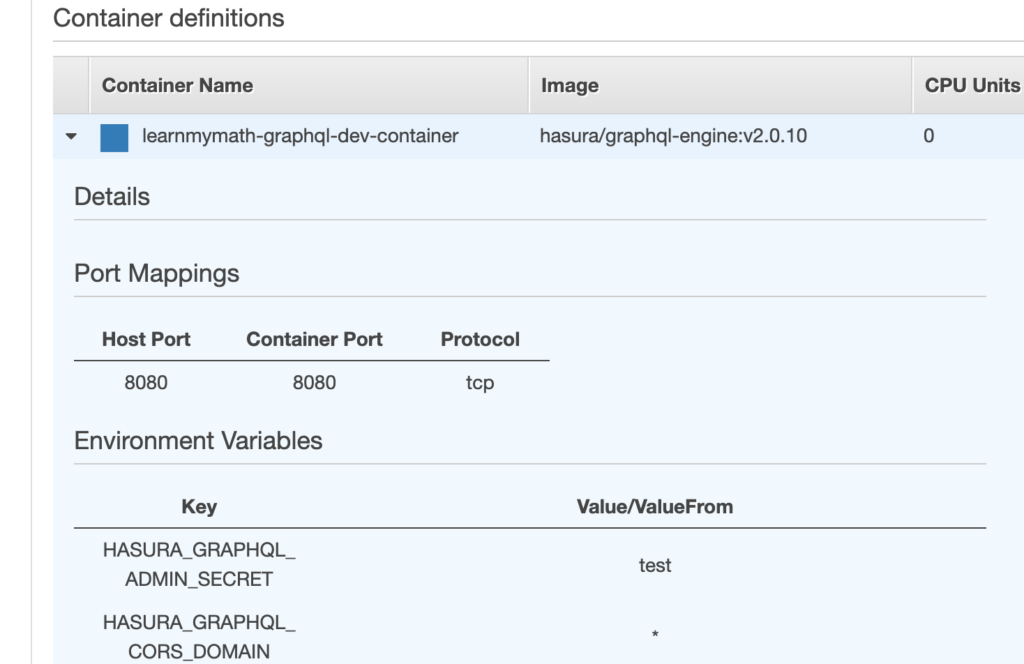
- Environment variables must be present
- Host port and Container port must be the same to work. I tried having container port different from host port and that did not work for me
- Size

- Leave “Operating system family” alone.
- Leave entrypoint or any command alone.
- Make sure that the ecs execution role has previliges to access other aws parties your app needs. Things such as secret manager, sqs, email, etc.
Create a Service using your Task Definition
- Fill in the Service details
- For security group, create a new security and make sure that group has access to and from database, third party APIs, or other aws services that call your service
- Make sure you only include AZ zones that are allowed by your load balancer.
- Add load balancer
- Add health check /ping
- Allow your server to boot up and be healthy before load balancer starts checking for its health
Hasura – Query
Hasura – Subscription
Hasura – Metadata