Data Structure and Algorithm
HashTable
The Hash table data structure stores elements in key-value pairs where
- Key– unique integer that is used for indexing the values
- Value – data that are associated with keys.
The key is sent to a hash function that performs arithmetic operations on it. The result (commonly called the hash value or hash) is the index of the key-value pair in the hash table.
1. Hash function
As we’ve already seen, the hash function determines the index of our key-value pair. Choosing an efficient hash function is a crucial part of creating a good hash table. You should always ensure that it’s a one-way function, i.e., the key cannot be retrieved from the hash. Another property of a good hash function is that it avoids producing the same hash for different keys.
2. Array
The array holds all the key-value entries in the table. The size of the array should be set according to the amount of data expected.
Collisions in hash tables & resolutions
A collision occurs when two keys get mapped to the same index. There are several ways of handling collisions.
1. Linear probing
If a pair is hashed to a slot which is already occupied, it searches linearly for the next free slot in the table.
2. Chaining
The hash table will be an array of linked lists. All keys mapping to the same index will be stored as linked list nodes at that index.
3. Resizing the hash table
The size of the hash table can be increased in order to spread the hash entries further apart. A threshold value signifies the percentage of the hash table that needs to be occupied before resizing. A hash table with a threshold of 0.6 would resize when 60% of the space is occupied. As a convention, the size of the hashtable is doubled. This can be memory intensive.
Time Complexity
| Operation | Average | Worst |
|---|---|---|
| Search | O(1) | O(n) |
| Insertion | O(1) | O(n) |
| Deletion | O(1) | O(n) |
| Space | O(n) | O(n) |
Strengths:
- Fast lookups. Lookups take time on average.
- Flexible keys. Most data types can be used for keys, as long as they’re hashable .
Weaknesses:
- Slow worst-case lookups. Lookups take time in the worst case .
- Unordered. Keys aren’t stored in a special order. If you’re looking for the smallest key, the largest key, or all the keys in a range, you’ll need to look through every key to find it.
- Single-directional lookups. While you can look up the value for a given key in time, looking up the keys for a given value requires looping through the whole dataset— time.
- Not cache-friendly. Many hash table implementations use linked lists , which don’t put data next to each other in memory.
public class MyHashMap<K, V> {
private int size = 10;
private MapNode<K, V>[] array = new MapNode[size];
public void put(K key, V value) {
int arrayIndex = hash(key);
putVal(key, value, arrayIndex);
}
private int hash(K key) {
int a = 20;
int b = 30;
int primeNumber = 101;
int m = size;
int h = key.hashCode();
return ((a * h * b) % primeNumber) % m;
}
public V get(K key) {
int arrayIndex = hash(key);
MapNode<K, V> head = array[arrayIndex];
if (head == null) {
return null;
}
MapNode<K, V> currentNode = head;
while (null != currentNode && !currentNode.getKey().equals(key)) {
currentNode = currentNode.getNext();
}
if (currentNode == null) {
return null;
} else {
return currentNode.getValue();
}
}
public void putVal(K key, V val, int arrayIndex) {
MapNode<K, V> head = array[arrayIndex];
if (head == null) {
array[arrayIndex] = head = new MapNode<>(key, val);
} else {
MapNode<K, V> currentNode = head;
MapNode<K, V> prevNode = head;
while (null != currentNode && !currentNode.getKey().equals(key)) {
prevNode = currentNode;
currentNode = currentNode.getNext();
}
if (currentNode == null) {
currentNode = new MapNode<>(key, val);
prevNode.setNext(currentNode);
} else {
currentNode.setValue(val);
}
}
}
}
@AllArgsConstructor
@ToString
@Data
public class MapNode<K, V> {
private K key;
private V value;
private MapNode<K, V> next;
public MapNode(K key, V value) {
this(key, value, null);
}
}
Graph
A graph data structure is a collection of nodes that have data and are connected to other nodes.
Let’s try to understand this through an example. On facebook, everything is a node. That includes User, Photo, Album, Event, Group, Page, Comment, Story, Video, Link, Note…anything that has data is a node.
Every relationship is an edge from one node to another. Whether you post a photo, join a group, like a page, etc., a new edge is created for that relationship.
A graph is a pair (V, E), where V is a set of nodes, called vertices, and E is a collection of pairs of vertices, called edges.
Applications of Graphs
- Representing relationships between components in electronic circuits
- Transportation networks: Highway network, Flight network
- Computer networks: Local area network, Internet, Web
- Databases: For representing ER (Entity Relationship) diagrams in databases, for
representing dependency of tables in databases
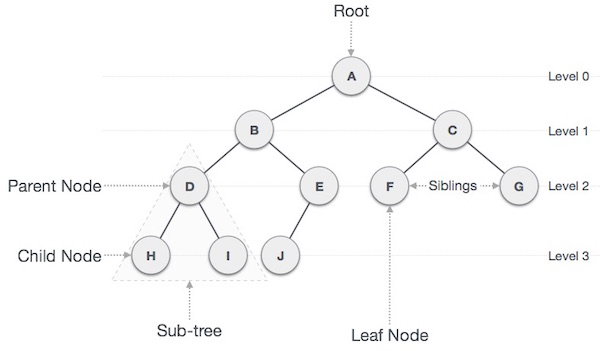
Trees
Tree is a data structure similar to a linked list but instead of each node pointing simply to the next node in a linear fashion, each node points to a number of nodes. Tree is an example of non- linear data structures. A tree structure is a way of representing the hierarchical nature of a structure in a graphical form.
A tree is a collection of entities called nodes. Nodes are connected by edges. Each node contains a value or data, and it may or may not have a child node
The first node of the tree is called the root. If this root node is connected by another node, the root is then a parent node and the connected node is a child.
Tree Properties:
- Root is the topmost
nodeof thetree - Edge is the link between two
nodes - Child is a
nodethat has aparent node - Parent is a
nodethat has anedgeto achild node - Leaf is a
nodethat does not have achild nodein thetree - Height is the length of the longest path to a
leaf - Depth is the length of the path to its
root
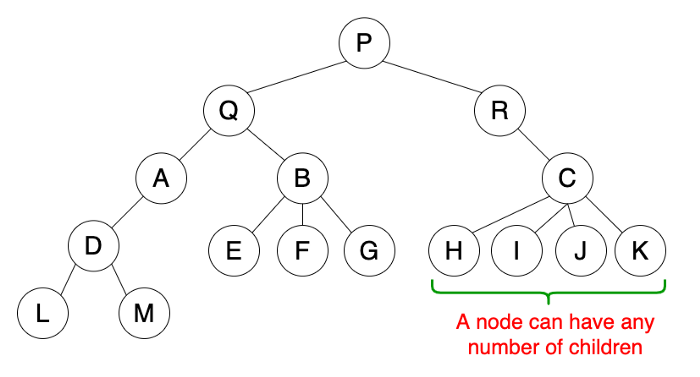
General Tree
A general tree is a tree data structure where there are no constraints on the hierarchical structure.
Properties
- Follow properties of a tree.
- A node can have any number of children.
Usage
- Used to store hierarchical data such as folder structures.
Types of Tree
- Binary Tree
- Binary Search Tree
- AVL Tree
- B-Tree
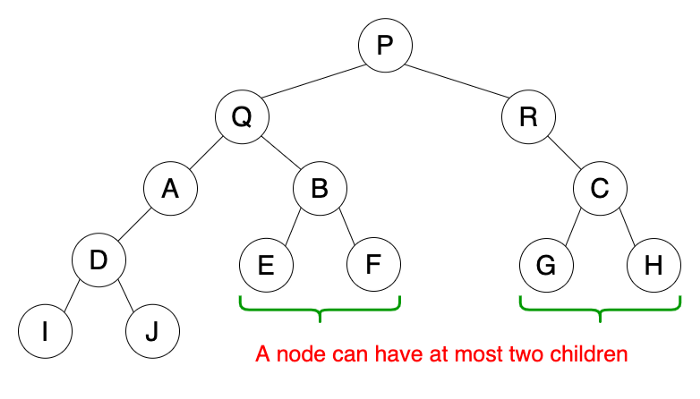
Binary Tree
A tree is called binary tree if each node has zero child, one child or two children. Empty tree is also a valid binary tree. We can visualize a binary tree as consisting of a root and two disjoint binary trees, called the left and right subtrees of the root.
Properties
- Follow properties of a tree.
- A node can have at most two child nodes (children).
- These two child nodes are known as the left child and right child.
-
A left child precedes a right child in the order of children of a node. Or in other others, left side of tree is small than right side of tree
Usage
- Used by compilers to build syntax trees.
- Used to implement expression parsers and expression solvers.
- Used to store router-tables in routers.
Note that Strict Binary Tree is a binary tree with each node has exactly two children or no children.
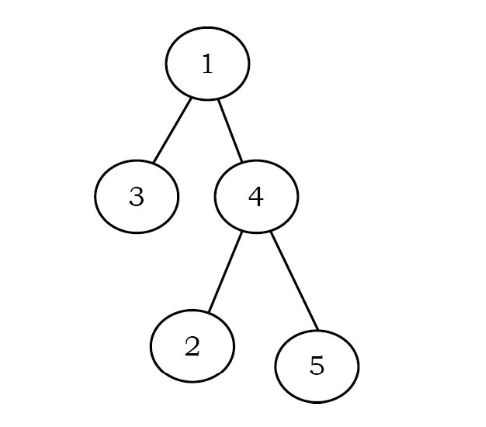
Full Binary Tree
A binary tree is called full binary tree if each node has exactly two children and all leaf nodes are at the same level.
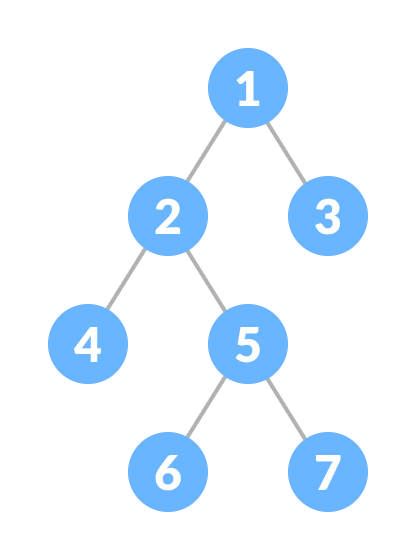
Complete Binary Tree
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Properties
1. Every level is filled, except the last level.
2. All nodes are filled starting from left
Applications of Binary Trees
Following are the some of the applications where binary trees play an important role:
-
- Expression trees are used in compilers.
- Huffman coding trees that are used in data compression algorithms.
- Binary Search Tree (BST), which supports search, insertion and deletion on a collection of items in O(logn) (average).
- Priority Queue (PQ), which supports search and deletion of minimum (or maximum)on a collection of items in logarithmic time (in worst case).
- Binary Search Trees(BSTs) are used to quickly check whether an element is present in a set or not.
- Heap is a kind of tree that is used for heap sort.
- A modified version of a tree called Tries is used in modern routers to store routing information.
- Most popular databases use B-Trees and T-Trees, which are variants of the tree structure we learned above to store their data
- Compilers use a syntax tree to validate the syntax of every program you write.
- In HTML, the Document Object Model (DOM) works as a tree.
@NoArgsConstructor
@AllArgsConstructor
@Data
@ToString
public class TreeNode {
private User data;
private TreeNode left;
private TreeNode right;
public TreeNode(User data) {
this.data = data;
}
}
@ToString
@NoArgsConstructor
@AllArgsConstructor
@Data
class User implements Serializable, Comparable<User> {
/**
*
*/
private static final long serialVersionUID = 1L;
private String name;
private Integer rating;
@Override
public int compareTo(User other) {
// TODO Auto-generated method stub
return this.rating.compareTo(other.getRating());
}
}
Insert data into Binary Tree
public TreeNode insert(TreeNode parent, User data) {
/**
* if node is null, put the data there
*/
if (parent == null) {
return new TreeNode(data);
}
User parentData = parent.getData();
/**
* if parent is greater than new node, go left<br>
* if parent is less than new node, go right<br>
*/
if (parentData.getRating() > data.getRating()) {
parent.setLeft(insert(parent.getLeft(), data));
} else {
parent.setRight(insert(parent.getRight(), data));
}
return parent;
}
public TreeNode insert(User data) {
if(root==null) {
root = new TreeNode(data);
return root;
}
return insert(root,data);
}
public class BinaryTreeMain {
public static void main(String[] args) {
// TODO Auto-generated method stub
TreeNode root = new TreeNode();
root.setData(new User("Folau", 20));
BinaryTree binaryTree = new BinaryTree(root);
binaryTree.insert(new User("Lisa", 30));
binaryTree.insert(new User("Laulau", 15));
binaryTree.insert(new User("Kinga", 12));
binaryTree.insert(new User("Fusi", 35));
binaryTree.insert(new User("Nesi", 34));
binaryTree.insert(new User("Melenesi", 32));
System.out.println("PreOrder Traversal");
binaryTree.preOrder(root, "root");
System.out.println("InOrder Traversal");
binaryTree.inOrder(root);
System.out.println("PostOrder Traversal");
binaryTree.postOrder(root);
}
}
PreOrder Traversal root - User(name=Folau, rating=20) left - User(name=Laulau, rating=15) left - User(name=Kinga, rating=12) right - User(name=Lisa, rating=30) right - User(name=Fusi, rating=35) left - User(name=Nesi, rating=34) left - User(name=Melenesi, rating=32) InOrder Traversal User(name=Kinga, rating=12) User(name=Laulau, rating=15) User(name=Folau, rating=20) User(name=Lisa, rating=30) User(name=Melenesi, rating=32) User(name=Nesi, rating=34) User(name=Fusi, rating=35) PostOrder Traversal User(name=Kinga, rating=12) User(name=Laulau, rating=15) User(name=Melenesi, rating=32) User(name=Nesi, rating=34) User(name=Fusi, rating=35) User(name=Lisa, rating=30) User(name=Folau, rating=20)
Now that inserting elements into binary tree is done. We have ways to navigate through or traverse a tree data structure.
We have two options. Breadth-First Search(BFS) and Depth-First Search(DFS)
Depth-First Search
DFS is an algorithm for traversing or searching tree data structure. One starts at the root and explores as far as possible along each branch before backtracking.
DFS explores a path all the way to a leaf before backtracking and exploring another path. There 3 types of DFS: pre-order, in-order, and post-order
Inorder traversal
- First, visit all the nodes in the left subtree
- Then the root node
- Visit all the nodes in the right subtree
Time Complexity: O(n). Space Complexity: O(n)
/**
* 1. Traverse the left subtree in Inorder.<br>
* 2. Visit the root.<br>
* 3. Traverse the right subtree in Inorder.<br>
* Time Complexity: O(n). Space Complexity: O(n).<br>
*/
public void inOrder(TreeNode node) {
if (node != null) {
inOrder(node.getLeft());
System.out.println(node.getData().toString());
inOrder(node.getRight());
}
}
Preorder traversal
- Visit root node
- Visit all the nodes in the left subtree
- Visit all the nodes in the right subtree
Time Complexity: O(n). Space Complexity: O(n)
/**
* 1. Visit the root.<br>
* 2. Traverse the left subtree in Preorder.<br>
* 3. Traverse the right subtree in Preorder.<br>
* Time Complexity: O(n). Space Complexity: O(n).
*/
public void preOrder(TreeNode node) {
if (node != null) {
System.out.println(node.getData().toString());
preOrder(node.getLeft());
preOrder(node.getRight());
}
}
Postorder traversal
- Visit all the nodes in the left subtree
- Visit all the nodes in the right subtree
- Visit the root node
Time Complexity: O(n). Space Complexity: O(n).
/**
* 1. Traverse the left subtree in Postorder.<br>
* 2. Traverse the right subtree in Postorder.<br>
* 3. Visit the root.<br>
* Time Complexity: O(n). Space Complexity: O(n).<br>
*/
public void postOrder(TreeNode node) {
if (node != null) {
postOrder(node.getLeft());
postOrder(node.getRight());
System.out.println(node.getData().toString());
}
}
Breadth-First Search
BFS is an algorithm for traversing or searching tree data structure. It starts at the tree root and explores the neighbor nodes first, before moving to the next level neighbors.
BFS algorithm traverses the tree level by level and depth by depth.
public void bfs() {
int level = 1;
queue.add(new LevelNode(root, level));
while (queue.isEmpty() != true) {
LevelNode levelNode = queue.poll();
TreeNode node = levelNode.getNode();
level++;
// 1. process node
System.out.println("level: "+levelNode.getLevel()+", data: "+ node.getData().toString());
// 2. push left and right child nodes onto queue
if(node.getLeft()!=null) {
queue.add(new LevelNode(node.getLeft(), level));
}
if(node.getRight()!=null) {
queue.add(new LevelNode(node.getRight(), level));
}
}
}
Heap
Heap is a tree-based data structure in which all the nodes of the tree are in a specific order. Heap is a complete binary tree-based data structure. Heaps have specific ordering properties. The ordering can be one of two types:
- Max-Heap: The value of a node must be greater than or equal to the values of its children. The greatest value is at the root. The same property must be true for all subtrees.
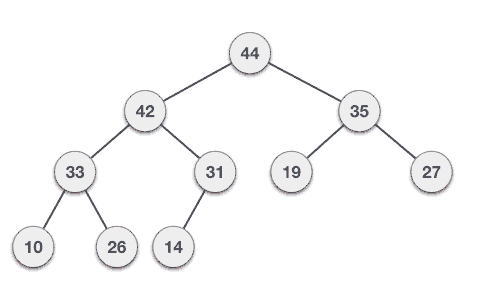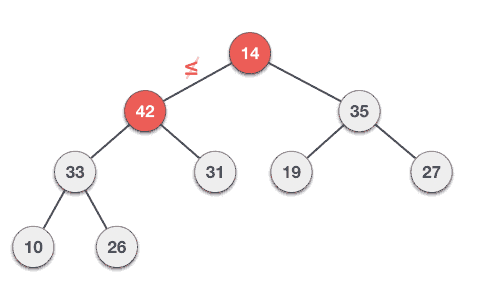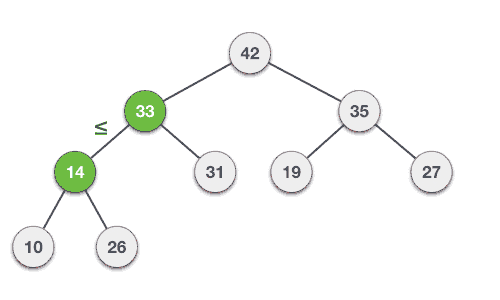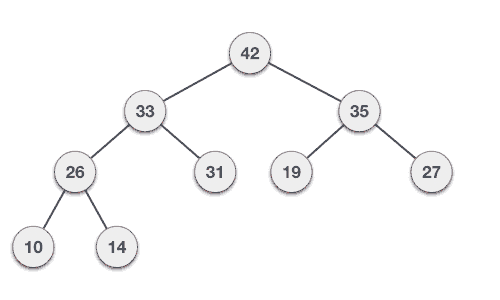
35 33 42 10 14 19 27 44 26 31
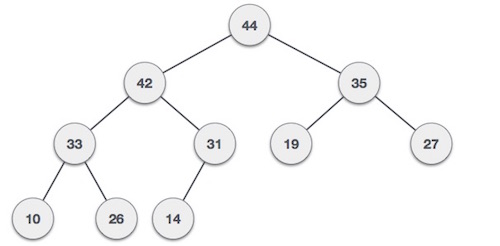
Max-Heap construction

Max-Heap deletion
@NoArgsConstructor @AllArgsConstructor @Data @ToString public class MaxHeap { private List<Integer> data = new ArrayList<>(); /** * Function to return the position of the parent for the node currently at position */ private int parent(int position) { if (position == 0) { return 0; } return (position - 1) / 2; } /** * Function to return the position of the left child for the node currently at position */ private int left(int position) { return (2 * position) + 1; } /** * Function to return the position of the right child for the node currently at position */ private int right(int position) { return (2 * position) + 2; } private void swap(int firstPosition, int secondPosition) { System.out.println("firstPosition: " + firstPosition + ", data: " + this.data.get(firstPosition) + ", secondPosition: " + secondPosition + ", data: " + this.data.get(secondPosition)); int tmp = this.data.get(firstPosition); this.data.set(firstPosition, this.data.get(secondPosition)); this.data.set(secondPosition, tmp); System.out.println("firstPosition: " + firstPosition + ", data: " + this.data.get(firstPosition) + ", secondPosition: " + secondPosition + ", data: " + this.data.get(secondPosition)); } public void add(int item) { this.data.add(item); // increase the size of an array Heap[++size] = element; int current = getSize() - 1; System.out.println("adding: " + item + " to position: " + current); heapifyUp(current); } public int peek() { return data.get(0); } /** * Step 1 − Remove root node.<br> * Step 2 − Move the last element of last level to root.<br> * Step 3 − Compare the value of this child node with its parent.<br> * Step 4 − If value of parent is less than child, then swap them.<br> * Step 5 − Repeat step 3 & 4 until Heap property holds.<br> */ public int poll() { int head = data.get(0); // replace the root of the heap with the last element data.set(0, this.data.get(getSize() - 1)); data.remove(getSize() - 1); // call heapify-down on the root node heapifyDown(0); return head; } /** * Step 1 − Create a new node at the end of heap.<br> * Step 2 − Assign new value to the node.<br> * Step 3 − Compare the value of this child node with its parent.<br> * Step 4 − If value of parent is less than child, then swap them.<br> * Step 5 − Repeat step 3 & 4 until Heap property holds.<br> */ private void heapifyUp(int position) { int temp = this.data.get(position); if (position > 0 && temp > this.data.get(parent(position))) { System.out.println("heapifyUp - position: " + position + ", data: " + this.data.get(parent(position))); // swap the two if heap property is violated swap(position, parent(position)); // call heapify-up on the parent heapifyUp(parent(position)); } } /** * Step 1 − Remove root node.<br> * Step 2 − Move the last element of last level to root.<br> * Step 3 − Compare the value of this child node with its parent.<br> * Step 4 − If value of parent is less than child, then swap them.<br> * Step 5 − Repeat step 3 & 4 until Heap property holds.<br> */ private void heapifyDown(int position) { int largest = position; int leftChild = left(position); int rightChild = right(position); // compare `A[i]` with its left and right child // and find the largest value int size = getSize(); if (leftChild < size && this.data.get(leftChild) > this.data.get(largest)) { largest = leftChild; } if (rightChild < size && this.data.get(rightChild) > this.data.get(largest)) { largest = rightChild; } if (largest != position) { // swap with a child having lesser value swap(position, largest); // call heapify-down on the child heapifyDown(largest); } } public void print() { System.out.println("\nList"); for (Integer d : data) { System.out.println("data: " + d); } System.out.println("\nTree"); System.out.println("Root: " + data.get(0)); for (int i = 1; i <= getSize() / 2; i++) { try { System.out.print("Parent: " + this.data.get(i - 1)); } catch (Exception e) { } try { System.out.print(", Left: " + this.data.get(this.left(i - 1))); } catch (Exception e) { } try { System.out.print(", Right: " + this.data.get((this.right(i - 1)))); } catch (Exception e) { } System.out.println(); } System.out.println("\n"); } public int getSize() { return this.data.size(); } } - Min-Heap: The value of a node is greater than or equal to the value of its parent. The smallest value is at the root. The same property must be true for all subtrees.
35 33 42 10 14 19 27 44 26 31
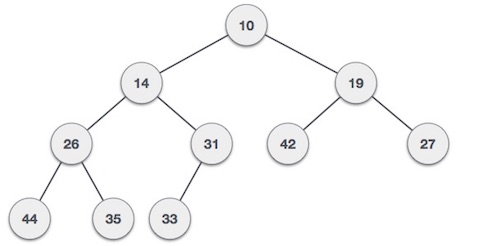
@NoArgsConstructor
@AllArgsConstructor
@Data
@ToString
public class MinHeap {
private List<Integer> data = new ArrayList<>();
/**
* Function to return the position of the parent for the node currently at position
*/
private int parent(int position) {
if (position == 0) {
return 0;
}
return (position - 1) / 2;
}
/**
* Function to return the position of the left child for the node currently at position
*/
private int left(int position) {
return (2 * position) + 1;
}
/**
* Function to return the position of the right child for the node currently at position
*/
private int right(int position) {
return (2 * position) + 2;
}
private void swap(int firstPosition, int secondPosition) {
System.out.println("firstPosition: " + firstPosition + ", data: " + this.data.get(firstPosition) + ", secondPosition: " + secondPosition + ", data: " + this.data.get(secondPosition));
int tmp = this.data.get(firstPosition);
this.data.set(firstPosition, this.data.get(secondPosition));
this.data.set(secondPosition, tmp);
System.out.println("firstPosition: " + firstPosition + ", data: " + this.data.get(firstPosition) + ", secondPosition: " + secondPosition + ", data: " + this.data.get(secondPosition));
}
public void add(int item) {
this.data.add(item);
// increase the size of an array Heap[++size] = element;
int current = getSize() - 1;
System.out.println("adding: " + item + " to position: " + current);
heapifyUp(current);
}
public int peek() {
return data.get(0);
}
public int poll() {
int head = data.get(0);
// replace the root of the heap with the last element
data.set(0, this.data.get(getSize() - 1));
data.remove(getSize() - 1);
// call heapify-down on the root node
heapifyDown(0);
return head;
}
/**
* Step 1 − Create a new node at the end of heap.<br>
* Step 2 − Assign new value to the node.<br>
* Step 3 − Compare the value of this child node with its parent.<br>
* Step 4 − If value of parent is greater than child, then swap them.<br>
* Step 5 − Repeat step 3 & 4 until Heap property holds.<br>
*/
private void heapifyUp(int position) {
int temp = this.data.get(position);
if (position > 0 && temp < this.data.get(parent(position))) {
System.out.println("heapifyUp - position: " + position + ", data: " + this.data.get(parent(position)));
// swap the two if heap property is violated
swap(position, parent(position));
// call heapify-up on the parent
heapifyUp(parent(position));
}
}
/**
* Step 1 − Remove root node.<br>
* Step 2 − Move the last element of last level to root.<br>
* Step 3 − Compare the value of this child node with its parent.<br>
* Step 4 − If value of parent is greater than child, then swap them.<br>
* Step 5 − Repeat step 3 & 4 until Heap property holds.<br>
*/
private void heapifyDown(int position) {
int smallest = position;
int leftChild = left(position);
int rightChild = right(position);
// compare `A[i]` with its left and right child
// and find the smallest value
int size = getSize();
if (leftChild < size && this.data.get(leftChild) < this.data.get(smallest)) {
smallest = leftChild;
}
if (rightChild < size && this.data.get(rightChild) < this.data.get(smallest)) {
smallest = rightChild;
}
if (smallest != position) {
// swap with a child having lesser value
swap(position, smallest);
// call heapify-down on the child
heapifyDown(smallest);
}
}
public void print() {
System.out.println("\nList");
for (Integer d : data) {
System.out.println("data: " + d);
}
System.out.println("\nTree");
System.out.println("Root: " + data.get(0));
for (int i = 1; i <= getSize() / 2; i++) {
try {
System.out.print("Parent: " + this.data.get(i - 1));
} catch (Exception e) {
}
try {
System.out.print(", Left: " + this.data.get(this.left(i - 1)));
} catch (Exception e) {
}
try {
System.out.print(", Right: " + this.data.get((this.right(i - 1))));
} catch (Exception e) {
}
System.out.println();
}
System.out.println("\n");
}
public int getSize() {
return this.data.size();
}
}
Heap Data Structure Applications
- Heap is used while implementing a priority queue.
- Dijkstra’s Algorithm
- Heap Sort
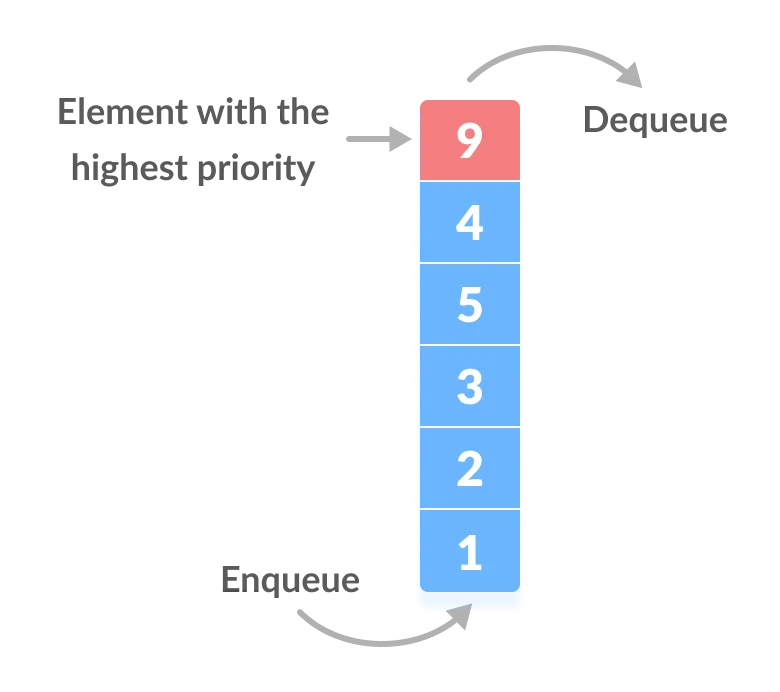
Priority Queue
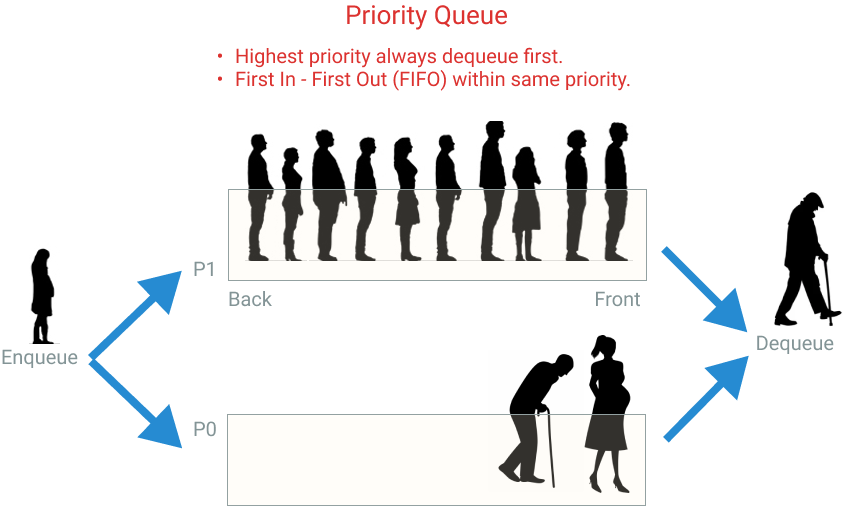
Priority queue is a data structure that extends the queue data structure with a priority dimension. Queue is a list of elements taken in the same order as they arrived. For instance, a line of people waiting to pay at the Supermarket behaves like a queue: first-in, first-served, or FIFO (first in, first out).
Priority queue adds a priority to each element’s value. If we go back to the example of a line of people in a supermarket. You can add preferred lanes, for example, Seniors (65+ years old) and pregnant women. If you have Seniors in the line, you will take them first, even if other people arrived before them. That’s what a priority queue (PQ) does. If all elements in a PQ have the same priority, then it will behave like a regular queue.
Applications of Priority Queue
There are many real-world applications for priority queues, such as:
- System to triage hospital patients and attend them by their severity order.
- Forward network packages in order of urgency (e.g., “real-time video call” should go before “time sync checks,” so to speak)
- Scheduling tasks in a system: “critical” goes before “shadow drawing” for instance.
- Asynchronous control flows like firing events (or notifying observers) in a certain order.
- Keeping track of top k elements efficiently
- Keeping track of median numbers in constant time
- Used in some graph algorithms like Dijkstra for finding the shortest path between two points. The distance among points is used as a priority.
Implementations
- Let’s explore several possibilities for data structures we could use to implement a priority queue:
- Unordered array
A simple, yet inefficient implementation, as retrieving the max element would require searching the entire array.
- Sorted array
This is not a very efficient implementation either. Inserting a new element requires linearly searching the array for the correct position. Removing similarly requires a linear time: the rest of the elements need to be adjusted (shifted) into correct positions.
- Hash table
Although inserting into a hash table takes constant time (given a good hash function), finding the max element takes linear time. Therefore, this would be a poor choice for the underlying data structure.
- Heap
It turns out that that a heap makes an efficient priority queue.
- Unordered array
| Operation | Unordered array | Sorted array | Hash table | Binary heap |
|---|---|---|---|---|
|
insert |
|
|
|
|
|
maxElement |
|
|
|
|
|
removeMaxElement |
|
|
|
|
public class MyPriorityQueueWithArray {
private int count = 0;
private int capacity = 10;
private PriorityNode[] elements = new PriorityNode[capacity];
public void enqueue(PriorityNode node) {
if (node == null || node.getData() == null) {
return;
}
System.out.println("node: " + node.toString());
System.out.println("count: " + count);
int position = 0;
if (count == 0) {
/**
* tail has the highest priority
*/
elements[position] = node;
} else {
PriorityNode highestNode = elements[position];
while (highestNode != null && node.getPriority() <= highestNode.getPriority()) {
position++;
highestNode = elements[position];
}
add(node, position);
}
System.out.println("insert position: " + position);
System.out.println("\n");
count++;
}
private void add(PriorityNode node, int position) {
if (count == capacity) {
/*
* when full, double its size
*/
capacity = capacity * 2;
}
PriorityNode[] temp = new PriorityNode[capacity];
int index = 0;
int lastIndex = count + 1;
while (index < lastIndex) {
if (index < position) {
/**
* front
*/
temp[index] = elements[index];
} else if (index == position) {
/**
* middle
*/
temp[position] = node;
} else {
/**
* back
*/
temp[index] = elements[index - 1];
}
index++;
}
elements = temp;
}
public PriorityNode removeAt(int position) {
PriorityNode[] temp = new PriorityNode[capacity];
PriorityNode removedNode = elements[position];
int index = 0;
int lastIndex = count + 1;
while (index < lastIndex) {
if (index < position) {
/**
* front
*/
System.out.println("front");
temp[index] = elements[index];
} else if (index == position) {
/**
* middle
*/
System.out.println("middle");
} else {
/**
* back
*/
System.out.println("back");
temp[index - 1] = elements[index];
}
if (temp[index] != null)
System.out.println("temp: " + temp[index].toString());
index++;
System.out.println("\n");
}
elements = temp;
return removedNode;
}
/**
* Retrieves, but does not remove, the head of this queue, or returns null if this queue is empty.
*/
public PriorityNode peek() {
return elements[0];
}
/**
* Retrieves and removes the head of this queue, or returns null if this queue is empty.
*/
public PriorityNode dequeue() {
return removeAt(0);
}
public void print() {
int index = 0;
PriorityNode node = elements[0];
while (node != null && count > index) {
System.out.println((index + 1) + ". " + node.toString());
index++;
node = elements[index];
}
}
}