Trees
Tree is a data structure similar to a linked list but instead of each node pointing simply to the next node in a linear fashion, each node points to a number of nodes. Tree is an example of non- linear data structures. A tree structure is a way of representing the hierarchical nature of a structure in a graphical form.
A tree is a collection of entities called nodes. Nodes are connected by edges. Each node contains a value or data, and it may or may not have a child node
The first node of the tree is called the root. If this root node is connected by another node, the root is then a parent node and the connected node is a child.
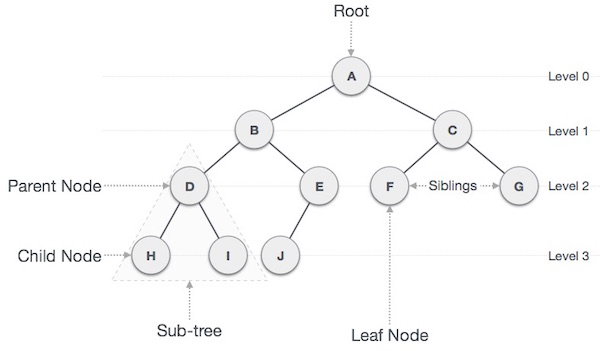
Tree Properties:
- Root is the topmost
nodeof thetree - Edge is the link between two
nodes - Child is a
nodethat has aparent node - Parent is a
nodethat has anedgeto achild node - Leaf is a
nodethat does not have achild nodein thetree - Height is the length of the longest path to a
leaf - Depth is the length of the path to its
root
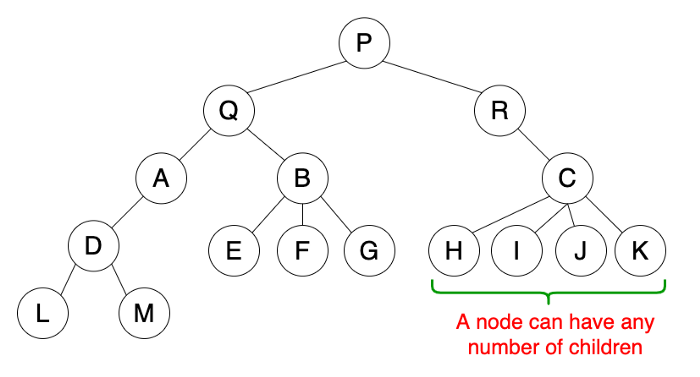
General Tree
A general tree is a tree data structure where there are no constraints on the hierarchical structure.
Properties
- Follow properties of a tree.
- A node can have any number of children.
Usage
- Used to store hierarchical data such as folder structures.
Types of Tree
- Binary Tree
- Binary Search Tree
- AVL Tree
- B-Tree
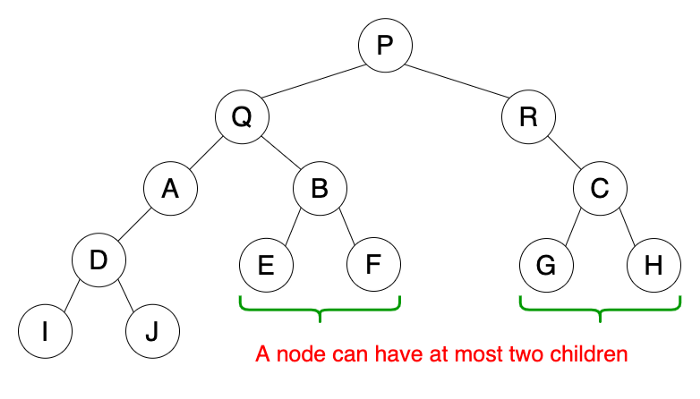
Binary Tree
A tree is called binary tree if each node has zero child, one child or two children. Empty tree is also a valid binary tree. We can visualize a binary tree as consisting of a root and two disjoint binary trees, called the left and right subtrees of the root.
Properties
- Follow properties of a tree.
- A node can have at most two child nodes (children).
- These two child nodes are known as the left child and right child.
-
A left child precedes a right child in the order of children of a node. Or in other others, left side of tree is small than right side of tree
Usage
- Used by compilers to build syntax trees.
- Used to implement expression parsers and expression solvers.
- Used to store router-tables in routers.
Note that Strict Binary Tree is a binary tree with each node has exactly two children or no children.
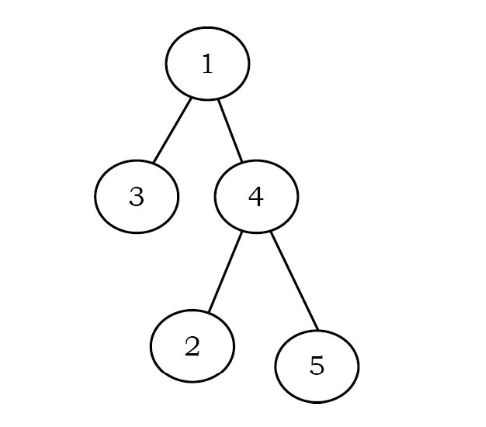
Full Binary Tree
A binary tree is called full binary tree if each node has exactly two children and all leaf nodes are at the same level.
Complete Binary Tree
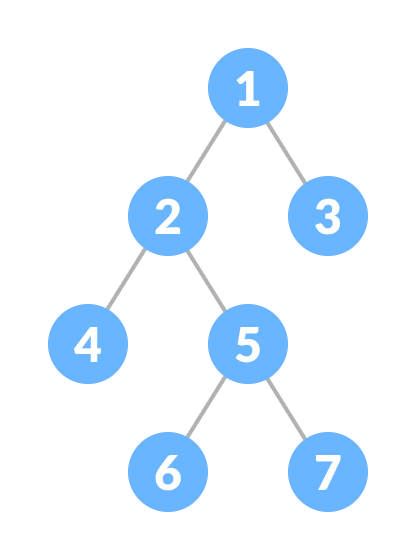
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Properties
1. Every level is filled, except the last level.
2. All nodes are filled starting from left
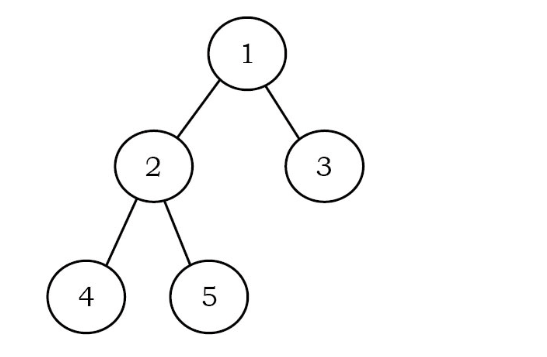
Applications of Binary Trees
Following are the some of the applications where binary trees play an important role:
-
- Expression trees are used in compilers.
- Huffman coding trees that are used in data compression algorithms.
- Binary Search Tree (BST), which supports search, insertion and deletion on a collection of items in O(logn) (average).
- Priority Queue (PQ), which supports search and deletion of minimum (or maximum)on a collection of items in logarithmic time (in worst case).
- Binary Search Trees(BSTs) are used to quickly check whether an element is present in a set or not.
- Heap is a kind of tree that is used for heap sort.
- A modified version of a tree called Tries is used in modern routers to store routing information.
- Most popular databases use B-Trees and T-Trees, which are variants of the tree structure we learned above to store their data
- Compilers use a syntax tree to validate the syntax of every program you write.
- In HTML, the Document Object Model (DOM) works as a tree.
@NoArgsConstructor
@AllArgsConstructor
@Data
@ToString
public class TreeNode {
private User data;
private TreeNode left;
private TreeNode right;
public TreeNode(User data) {
this.data = data;
}
}
@ToString
@NoArgsConstructor
@AllArgsConstructor
@Data
class User implements Serializable, Comparable<User> {
/**
*
*/
private static final long serialVersionUID = 1L;
private String name;
private Integer rating;
@Override
public int compareTo(User other) {
// TODO Auto-generated method stub
return this.rating.compareTo(other.getRating());
}
}
Insert data into Binary Tree
public TreeNode insert(TreeNode parent, User data) {
/**
* if node is null, put the data there
*/
if (parent == null) {
return new TreeNode(data);
}
User parentData = parent.getData();
/**
* if parent is greater than new node, go left<br>
* if parent is less than new node, go right<br>
*/
if (parentData.getRating() > data.getRating()) {
parent.setLeft(insert(parent.getLeft(), data));
} else {
parent.setRight(insert(parent.getRight(), data));
}
return parent;
}
public TreeNode insert(User data) {
if(root==null) {
root = new TreeNode(data);
return root;
}
return insert(root,data);
}
public class BinaryTreeMain {
public static void main(String[] args) {
// TODO Auto-generated method stub
TreeNode root = new TreeNode();
root.setData(new User("Folau", 20));
BinaryTree binaryTree = new BinaryTree(root);
binaryTree.insert(new User("Lisa", 30));
binaryTree.insert(new User("Laulau", 15));
binaryTree.insert(new User("Kinga", 12));
binaryTree.insert(new User("Fusi", 35));
binaryTree.insert(new User("Nesi", 34));
binaryTree.insert(new User("Melenesi", 32));
System.out.println("PreOrder Traversal");
binaryTree.preOrder(root, "root");
System.out.println("InOrder Traversal");
binaryTree.inOrder(root);
System.out.println("PostOrder Traversal");
binaryTree.postOrder(root);
}
}
PreOrder Traversal root - User(name=Folau, rating=20) left - User(name=Laulau, rating=15) left - User(name=Kinga, rating=12) right - User(name=Lisa, rating=30) right - User(name=Fusi, rating=35) left - User(name=Nesi, rating=34) left - User(name=Melenesi, rating=32) InOrder Traversal User(name=Kinga, rating=12) User(name=Laulau, rating=15) User(name=Folau, rating=20) User(name=Lisa, rating=30) User(name=Melenesi, rating=32) User(name=Nesi, rating=34) User(name=Fusi, rating=35) PostOrder Traversal User(name=Kinga, rating=12) User(name=Laulau, rating=15) User(name=Melenesi, rating=32) User(name=Nesi, rating=34) User(name=Fusi, rating=35) User(name=Lisa, rating=30) User(name=Folau, rating=20)
Now that inserting elements into binary tree is done. We have ways to navigate through or traverse a tree data structure.
We have two options. Breadth-First Search(BFS) and Depth-First Search(DFS)
Depth-First Search
DFS is an algorithm for traversing or searching tree data structure. One starts at the root and explores as far as possible along each branch before backtracking.
DFS explores a path all the way to a leaf before backtracking and exploring another path. There 3 types of DFS: pre-order, in-order, and post-order
Inorder traversal
- First, visit all the nodes in the left subtree
- Then the root node
- Visit all the nodes in the right subtree
Time Complexity: O(n). Space Complexity: O(n)
/**
* 1. Traverse the left subtree in Inorder.<br>
* 2. Visit the root.<br>
* 3. Traverse the right subtree in Inorder.<br>
* Time Complexity: O(n). Space Complexity: O(n).<br>
*/
public void inOrder(TreeNode node) {
if (node != null) {
inOrder(node.getLeft());
System.out.println(node.getData().toString());
inOrder(node.getRight());
}
}
Preorder traversal
- Visit root node
- Visit all the nodes in the left subtree
- Visit all the nodes in the right subtree
Time Complexity: O(n). Space Complexity: O(n)
/**
* 1. Visit the root.<br>
* 2. Traverse the left subtree in Preorder.<br>
* 3. Traverse the right subtree in Preorder.<br>
* Time Complexity: O(n). Space Complexity: O(n).
*/
public void preOrder(TreeNode node) {
if (node != null) {
System.out.println(node.getData().toString());
preOrder(node.getLeft());
preOrder(node.getRight());
}
}
Postorder traversal
- Visit all the nodes in the left subtree
- Visit all the nodes in the right subtree
- Visit the root node
Time Complexity: O(n). Space Complexity: O(n).
/**
* 1. Traverse the left subtree in Postorder.<br>
* 2. Traverse the right subtree in Postorder.<br>
* 3. Visit the root.<br>
* Time Complexity: O(n). Space Complexity: O(n).<br>
*/
public void postOrder(TreeNode node) {
if (node != null) {
postOrder(node.getLeft());
postOrder(node.getRight());
System.out.println(node.getData().toString());
}
}
Breadth-First Search
BFS is an algorithm for traversing or searching tree data structure. It starts at the tree root and explores the neighbor nodes first, before moving to the next level neighbors.
BFS algorithm traverses the tree level by level and depth by depth.
public void bfs() {
int level = 1;
queue.add(new LevelNode(root, level));
while (queue.isEmpty() != true) {
LevelNode levelNode = queue.poll();
TreeNode node = levelNode.getNode();
level++;
// 1. process node
System.out.println("level: "+levelNode.getLevel()+", data: "+ node.getData().toString());
// 2. push left and right child nodes onto queue
if(node.getLeft()!=null) {
queue.add(new LevelNode(node.getLeft(), level));
}
if(node.getRight()!=null) {
queue.add(new LevelNode(node.getRight(), level));
}
}
}