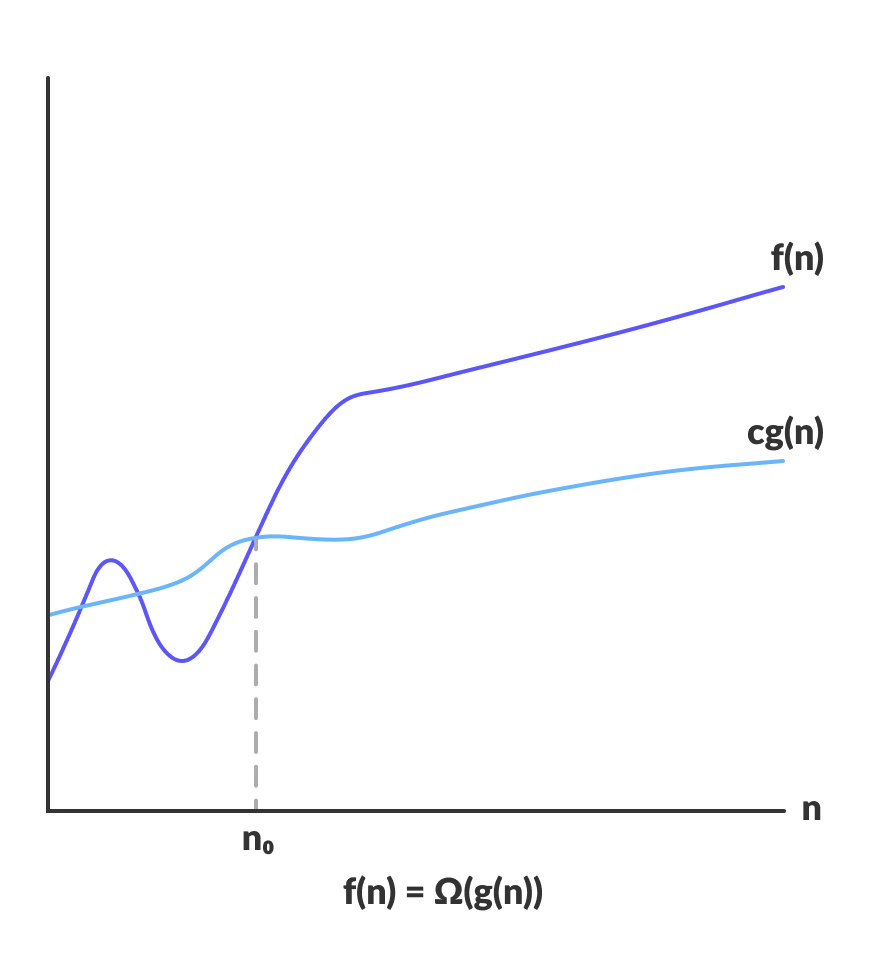
Big Omega Notation
The Omega notation represents the lower bound of the running time of an algorithm. It provides the best case complexity of an algorithm.
So if we represent a complexity of an algorithm in Omega notation, it means that the algorithm cannot be completed in less time than this, it would at least take the time represented by Omega notation or it can take more (when not in best case scenario).
For example:
f(n) = 3n + 2
g(n) = n
If we want to represent f(n) as Ω(g(n)) then it must satisfy f(n) >= C g(n) for all values of C > 0 and n0>= 1
f(n) >= C g(n)
⇒3n + 2 >= C n
Above condition is always TRUE for all values of C = 1 and n >= 1.
By using Big – Omega notation we can represent the time complexity as follows.
3n + 2 = Ω(n)