Dynamic Programming
Dynamic programming is similar to Divide and Conquer in in that a problem is broken down into smaller sub-problems. But unlike, Divide and Conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are stored and used for similar or overlapping sub-problems.
Note that the difference between Dynamic Programming and straightforward recursion is in memoization of recursive calls. If the sub problems are independent and there is no repetition then memoization does not help, so dynamic programming is not a solution for all problems.
Dynamic programming is used where we have problems, which can be divided into similar sub-problems, so that their results can be re-used. Mostly, these algorithms are used for optimization. Before solving the in-hand sub-problem, dynamic algorithm will try to examine the results of the previously solved sub-problems. The solutions of sub-problems are combined in order to achieve the best solution.
Dynamic programming takes the brute force approach. It Identifies repeated work, and eliminates repetition.
Dynamic Programming Strategy
- Divide – breaking the problem into smaller sub-problems.
- Conquer – solve the problem if it’s small enough(base case) or check cache to see if a simpler problem has been solved and use that answer. If the problem is still not small enough, divide it into smaller problems solve them.
- Combine – combine solutions from subproblems and generate a solution for the original problem.
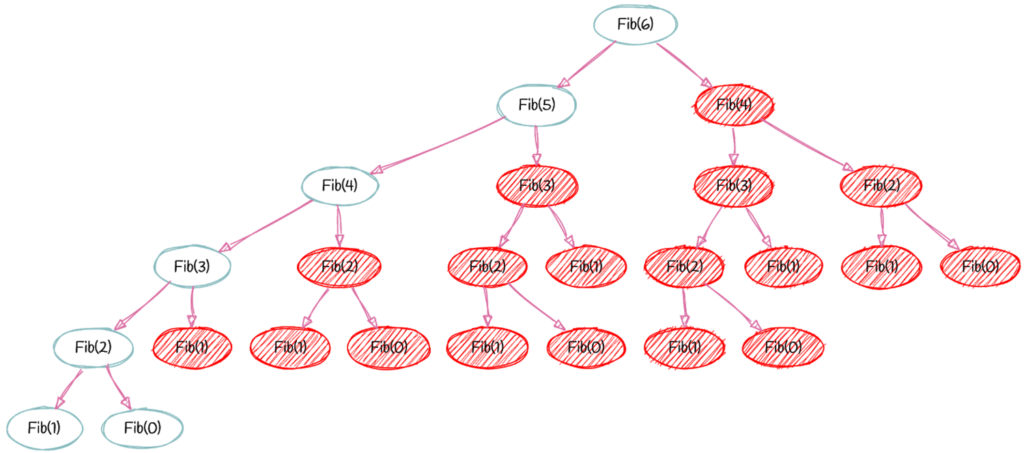
Dynamic programming can be used in both bottom-up(Tabulation) and top-down(Memoization) manner. And of course, most of the times, referring to the previous solution output is cheaper than recomputing in terms of CPU cycles.
Bottom-up(Tabulation) Dynamic Programming
We evaluate the function starting with the smallest possible input argument value and then we step through possible values, slowly increasing the input argument value. While computing the values we store all computed values in a table (memory). As larger arguments are evaluated, pre-computed values for smaller arguments can be used.
Tabulation is the opposite of the top-down approach and avoids recursion. In this approach, we solve the problem “bottom-up” (i.e. by solving all the related sub-problems first). This is typically done by filling up an n-dimensional table. Based on the results in the table, the solution to the top/original problem is then computed.
Tabulation is the opposite of Memoization, as in Memoization we solve the problem and maintain a map of already solved sub-problems. In other words, in memoization, we do it top-down in the sense that we solve the top problem first (which typically recurses down to solve the sub-problems).
/**
* Dynamic Programming with Tabulation<br>
*/
public static int fibonacciWithTabulation(int num) {
if (num <= 0) {
return 0;
}
int storage[] = new int[num + 1];
/**
* first and second case are pre-computed
*/
/*
* first case
*/
storage[0] = 0;
/*
* second case
*/
storage[1] = 1;
for (int i = 2; i <= num; i++) {
storage[i] = storage[i - 1] + storage[i - 2];
System.out.println(storage[i - 1] + "+" + storage[i - 2] + " = " + storage[i]);
}
return storage[num];
}
Top-down(Memoization) Dynamic Programming
The problem is broken into sub problems, each of these sub problems is solved, and the solutions are remembered or stored in memory(Map). If this function is called twice with the same parameters, you simply look up the answer in the storage(Map). As the first action you check if pre-computed value exists in storage. if it does exist use in the storage, use or return that value, if it does not compute it or divide it again.
Here is an example.
/**
* Dynamic Programming with Memoization<br>
* storage can be a map, array, or list depending on your situation.
*/
private static int fibonacciWithCache(Map<Integer, Integer> storage, int num) {
if (num <= 1) {
return num;
}
if (storage.containsKey(num)) {
return storage.get(num);
}
int number1 = fibonacciWithCache(storage,num - 1);
int number2 = fibonacciWithCache(storage,num - 2);
int result = number1 + number2;
storage.put(num, result);
return result;
}
When do you use Divide and Conquer?
When we see problems like:
- shortest/longest
- minimized/maximized
- least/most,
- fewest/greatest
- biggest/smallest
These kinds of problems are optimisation problems.
How to solve a problem with Dynamic Programming
Imagine you have found a problem that’s an optimisation problem, but you are not sure if it can be solved with Dynamic Programming. First, identify what you are optimising for. Once you realize what you are optimising for, you have to decide how easy it is to perform that optimisation. Sometimes, the greedy approach is enough for an optimal solution.
Before we even start to plan the problem as a dynamic programming problem, think about what the brute force solution might look like. Are sub steps repeated in the brute-force solution? If so, we try to imagine the problem as a dynamic programming problem.
Mastering dynamic programming is all about understanding the problem. List all the inputs that can affect the answers. Once we’ve identified all the inputs and outputs, try to identify whether the problem can be broken into subproblems. If we can identify subproblems, we can probably use Dynamic Programming.
Then, figure out what the recurrence is and solve it. When we’re trying to figure out the recurrence, remember that whatever recurrence we write has to help us find the answer. Sometimes the answer will be the result of the recurrence, and sometimes we will have to get the result by looking at a few results from the recurrence.
Dynamic Programming can solve many problems, but that does not mean there isn’t a more efficient solution out there. Solving a problem with Dynamic Programming feels like magic, but remember that dynamic programming is merely a clever brute force. Sometimes it pays off well, and sometimes it helps only a little.
Where is Divide and Conquer being used?
- Many string algorithms including longest common subsequence, longest increasing subsequence, longest common substring, edit distance.
- Algorithms on graphs can be solved efficiently: Bellman-Ford algorithm for finding the shortest distance in a graph, Floyd’s All-Pairs shortest path algorithm, etc.
- Chain matrix multiplication
- Subset Sum
- 0/1 Knapsack
- Travelling salesman problem, and many more