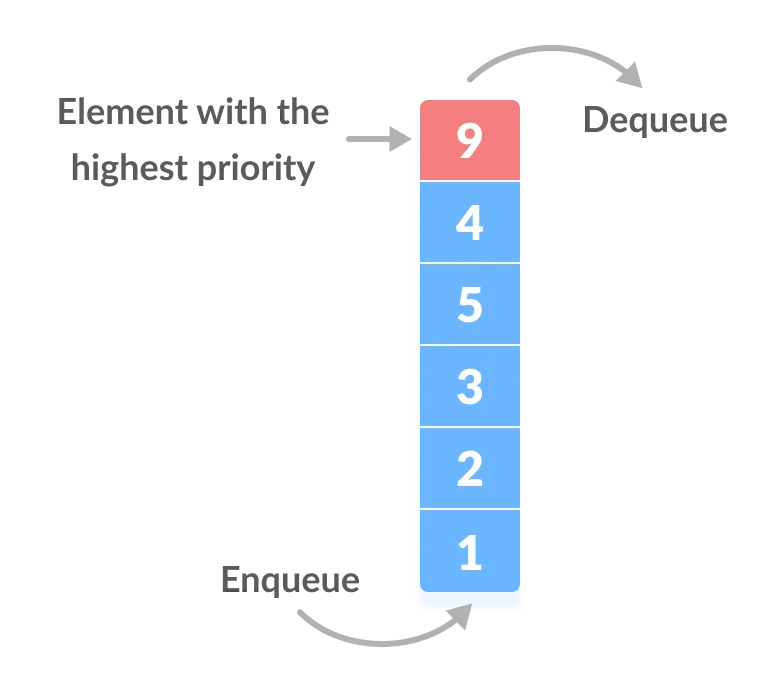
Priority queue is a data structure that extends the queue data structure with a priority dimension. Queue is a list of elements taken in the same order as they arrived. For instance, a line of people waiting to pay at the Supermarket behaves like a queue: first-in, first-served, or FIFO (first in, first out).

Priority queue adds a priority to each element’s value. If we go back to the example of a line of people in a supermarket. You can add preferred lanes, for example, Seniors (65+ years old) and pregnant women. If you have Seniors in the line, you will take them first, even if other people arrived before them. That’s what a priority queue (PQ) does. If all elements in a PQ have the same priority, then it will behave like a regular queue.

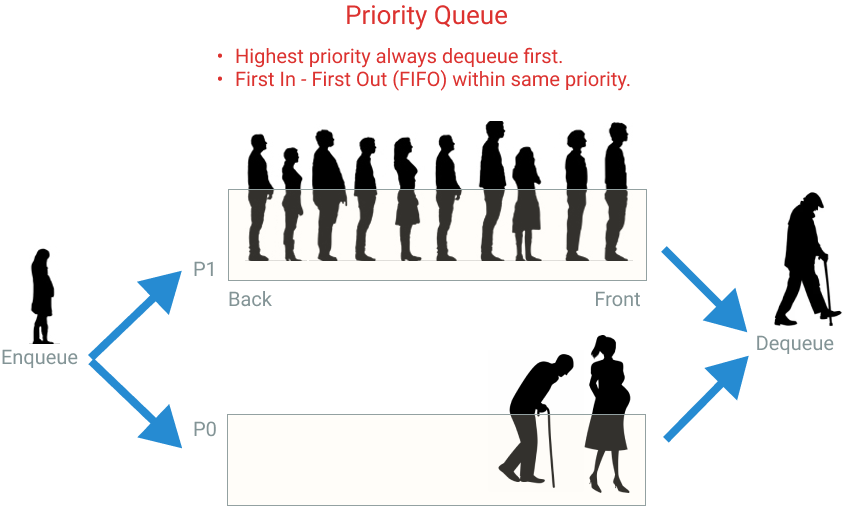
Applications of Priority Queue

There are many real-world applications for priority queues, such as:

• System to triage hospital patients and attend them by their severity order.
• Forward network packages in order of urgency (e.g., “real-time video call” should go before “time sync checks,” so to speak)
• Scheduling tasks in a system: “critical” goes before “shadow drawing” for instance.
• Asynchronous control flows like firing events (or notifying observers) in a certain order.
• Keeping track of top k elements efficiently
• Keeping track of median numbers in constant time
• Used in some graph algorithms like Dijkstra for finding the shortest path between two points. The distance among points is used as a priority.

Implementations

public class MyPriorityQueueWithArray {

    private int            count    = 0;
    private int            capacity = 10;
    private PriorityNode[] elements = new PriorityNode[capacity];

    public void enqueue(PriorityNode node) {
        if (node == null || node.getData() == null) {
            return;
        }
        System.out.println("node: " + node.toString());
        System.out.println("count: " + count);

        int position = 0;

        if (count == 0) {

            /**
             * tail has the highest priority
             */
            elements[position] = node;

        } else {

            PriorityNode highestNode = elements[position];

            while (highestNode != null && node.getPriority() <= highestNode.getPriority()) {

                position++;
                highestNode = elements[position];

            }

            add(node, position);

        }

        System.out.println("insert position: " + position);
        System.out.println("\n");
        count++;
    }

    private void add(PriorityNode node, int position) {

        if (count == capacity) {
            /*
             * when full, double its size
             */
            capacity = capacity * 2;
        }

        PriorityNode[] temp = new PriorityNode[capacity];

        int index = 0;
        int lastIndex = count + 1;

        while (index < lastIndex) {

            if (index < position) {
                /**
                 * front
                 */
                temp[index] = elements[index];
            } else if (index == position) {
                /**
                 * middle
                 */
                temp[position] = node;
            } else {
                /**
                 * back
                 */
                temp[index] = elements[index - 1];
            }

            index++;
        }

        elements = temp;
    }

    public PriorityNode removeAt(int position) {

        PriorityNode[] temp = new PriorityNode[capacity];

        PriorityNode removedNode = elements[position];

        int index = 0;
        int lastIndex = count + 1;

        while (index < lastIndex) {

            if (index < position) {
                /**
                 * front
                 */
                System.out.println("front");
                temp[index] = elements[index];
            } else if (index == position) {
                /**
                 * middle
                 */
                System.out.println("middle");
            } else {
                /**
                 * back
                 */
                System.out.println("back");
                temp[index - 1] = elements[index];
            }
            if (temp[index] != null)
                System.out.println("temp: " + temp[index].toString());

            index++;
            System.out.println("\n");
        }

        elements = temp;

        return removedNode;
    }

    /**
     * Retrieves, but does not remove, the head of this queue, or returns null if this queue is empty.
     */
    public PriorityNode peek() {
        return elements[0];
    }

    /**
     * Retrieves and removes the head of this queue, or returns null if this queue is empty.
     */
    public PriorityNode dequeue() {
        return removeAt(0);
    }

    public void print() {
        int index = 0;
        PriorityNode node = elements[0];
        while (node != null && count > index) {
            System.out.println((index + 1) + ". " + node.toString());
            index++;
            node = elements[index];
        }
    }
}

Source code on Github