Binary Search
Write a function that takes in a sorted array of integers as well as a target integer. The function should use the Binary Search algorithm to determine if the target integer is contained in the array and should return its index if it is, otherwise -1.
I have a solution here.
Quick Sort
Write a function that takes in an array of integers and returns a sorted version of that array. Use the Quick Sort algorithm to sort the array.
I have a solution here.
Three Number Sum
Write a function that takes in a non-empty array of distinct integers and an integer representing a target sum. The function should find all triplets in the array that sum up to the target sum and return a two-dimensional array of all these triplets. The numbers in each triplet should be ordered in ascending order, and the triplets themselves should be ordered in ascending order with respect to the numbers they hold.
If no three numbers sum up to the target sum, the function should return an empty array.
Time complexity: O(n^2)
Space complexity: O(n)
public static List<Integer[]> threeNumberSum(int[] array, int targetSum) {
int size = array.length;
List<Integer[]> answers = new ArrayList<>();
if (size < 2) {
return answers;
}
Arrays.sort(array);
for (int x = 0; x < size - 2; x++) {
int left = x + 1;
int right = size - 1;
while (left < right) {
int sum = array[x] + array[left] + array[right];
if (sum == targetSum) {
Integer[] triplet = {array[x], array[left], array[right]};
answers.add(triplet);
left++;
right--;
} else if (sum < targetSum) {
left++;
} else if (sum > targetSum) {
right--;
}
}
}
return answers;
}
Two Number Sum
Write a function that takes in a non-empty array of distinct integers and an integer representing a target sum. If any two numbers in the input array sum up to the target sum, the function should return them in an array, in any order. If no two numbers sum up to the target sum, the function should return
an empty array.
Note that the target sum has to be obtained by summing two different integers in the array; you can’t add a single integer to itself in order to obtain the
target sum.
Sometimes you need to return the indices of the two numbers instead of the two numbers.
First attempt using 2 for loops
Time complexity: O(n^2)
Space complexity: O(1)
public static int[] twoNumberSum(int[] array, int targetSum) {
int size = array.length;
if (size < 2) {
return new int[0];
}
for (int x = 0; x < size; x++) {
for (int y = 0; y < size; y++) {
if (x == y) {
continue;
}
if (array[x] + array[y] == targetSum) {
int[] operands = new int[2];
operands[0] = array[x];
operands[1] = array[y];
return operands;
}
}
}
return new int[0];
}
Second attempt with a sorted Array
Time complexity: O(nlogn)
Space complexity: O(1)
if space is more important than time, this is the optimal solution.
public static int[] twoNumberSum(int[] array, int targetSum) {
int size = array.length;
if (size < 2) {
return new int[0];
}
Arrays.sort(array);
int left = 0;
int right = size - 1;
while (left < right) {
int sum = array[left] + array[right];
if (sum == targetSum) {
return new int[]{array[left], array[right]};
} else if (sum < targetSum) {
left++;
} else if (sum > targetSum) {
right--;
}
}
return new int[0];
}
Third attempt with a Set
Time complexity: O(n)
Space complexity: O(n)
if time is more important than space, this is the optimal solution.
public static int[] twoNumberSum(int[] array, int targetSum) {
int size = array.length;
if (size < 2) {
return new int[0];
}
Map<Integer> nums = new HashMap<>();
for (int num : array) {
int match = targetSum - num;
if (nums.containsKey(match)) {
return new int[]{match, num};
} else {
nums.put(num,num);
}
}
return new int[0];
}
Binary Search
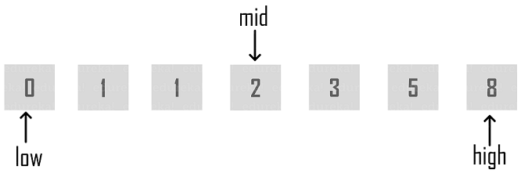
Binary Search is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. It works only on a sorted set of elements. To use binary search on a collection, the collection must first be sorted.
When the binary search is used to perform operations on a sorted set, the number of iterations can always be reduced on the basis of the value that is being searched. You can see in the below snapshot of finding the mid element. The analogy of binary search is to use the information that the array is sorted and reduce the time complexity to O(log n).
Advantages
- A binary search algorithm is a fairly simple search algorithm to implement.
- It is a significant improvement over linear search and performs almost the same in comparison to some of the harder to implement search algorithms.
- The binary search algorithm breaks the list down in half on every iteration, rather than sequentially combing through the list. On large lists, this method can be really useful.
Note that the array has to be sorted.
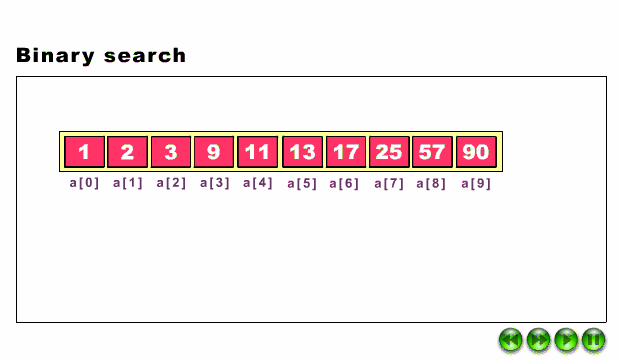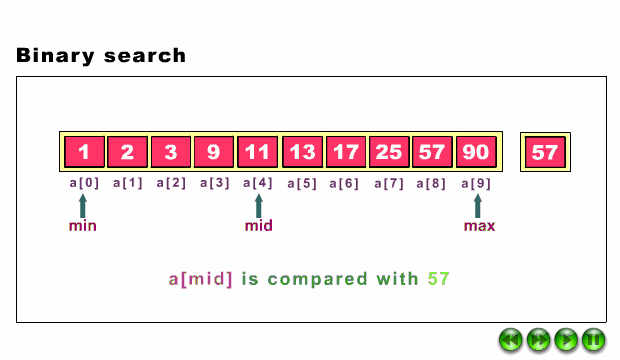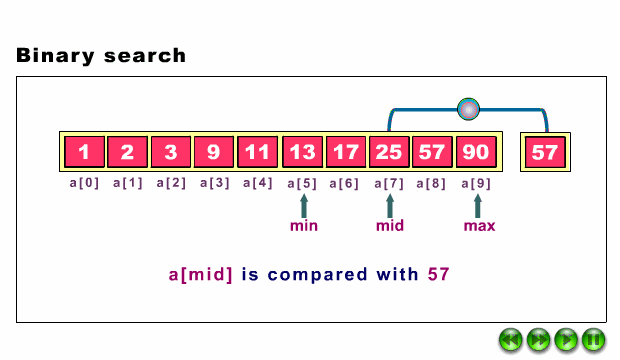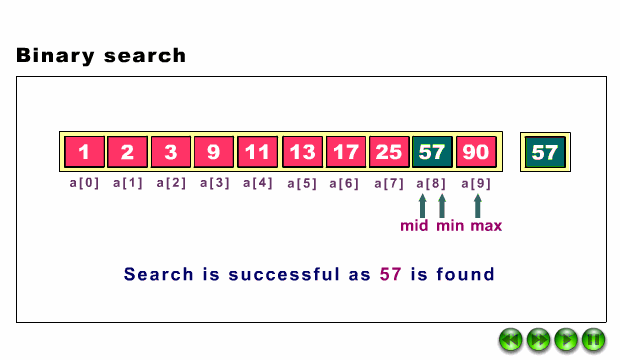
Binary Search in a iterative way
Time: O(log n)
Space: O(log n) or O(1)
public int search(int array[], int searchElement, int lowIndex, int highIndex) {
// Repeat until the pointers low and high meet each other
while (lowIndex <= highIndex) {
// get index of mid element
int midIndex = lowIndex + (highIndex - lowIndex) / 2;
int midValue = array[midIndex];
// if element to be searched is the mid element
if (midValue == searchElement) {
return midIndex;
}
// if element is less than mid element
// search only the left side of mid
if (midValue < searchElement) {
lowIndex = midIndex + 1;
// if element is greater than mid element
// search only the right side of mid
} else {
highIndex = midIndex - 1;
}
}
return -1;
}
Notice how the middle index is generated (int mid = low + ((high – low) / 2). This to accommodate for extremely large arrays. If the middle index is generated simply by getting the middle index (int mid = (low + high) / 2), an overflow may occur for an array containing 230 or more elements as the sum of low + high could easily exceed the maximum positive int value.
Binary Search in a recursive way
Time: O(log n)
Space: O(log n)
public int search(int array[], int searchElement, int lowIndex, int highIndex) {
if (highIndex >= lowIndex) {
int midIndex = lowIndex + (highIndex - lowIndex) / 2;
int midValue = array[midIndex];
// check if mid element is searched element
if (midValue == searchElement) {
return midIndex;
}
// Search the left half of mid
if (midValue > searchElement) {
return searchWithRecursion(array, searchElement, lowIndex, midIndex - 1);
}
// Search the right half of mid
return searchWithRecursion(array, searchElement, midIndex + 1, highIndex);
}
return -1;
}
Tests
CustomBinarySearch bs = new CustomBinarySearch();
int[] numbers = {1, 4, 6, 45, 367};
Arrays.sort(numbers);
int searchNumber = 6;
int searchNumberIndex = bs.search(numbers, searchNumber, 0, numbers.length - 1);
System.out.println("searchNumber: " + searchNumber + ", searchNumberIndex: " + searchNumberIndex);
searchNumberIndex = bs.searchWithRecursion(numbers, searchNumber, 0, numbers.length - 1);
System.out.println("searchNumber: " + searchNumber + ", searchNumberIndex: " + searchNumberIndex);
Is it better to do a recursive binary search or an iterative binary search?
The recursive version of Binary Search has a space complexity of O(log N), but the iterative version has a space complexity of O(log N) (1). As a result, while the recursive version is simple to build, the iterative form is more efficient.
- Recursion can be slower due to the overhead of maintaining a stack and usually takes up more memory
- Recursion is not stack-friendly. It may cause StackOverflowException when processing big data sets
- Recursion adds clarity to the code as it makes it shorter in comparison to the iterative approach
Ideally, a binary search will perform less number of comparisons in contrast to a linear search for large values of n. For smaller values of n, the linear search could perform better than a binary search.
One should know that this analysis is theoretical and might vary depending on the context.
Using binary search in java
Binary search with java array
int index = Arrays.binarySearch(sortedArray, key);
Binary search with java collection
int index = Collections.binarySearch(sortedList, key);