Depth-First Search
Breadth-First Search
Quick Sort
QuickSort is a Divide and Conquer algorithm. It picks an element as pivot and partitions the given array around the picked pivot. There are many different versions of quickSort that pick pivot in different ways.
- Always pick first element as pivot.
- Always pick last element as pivot (implemented below)
- Pick a random element as pivot.
- Pick median as pivot.
The key process in quickSort is partition(). Target of partitions is, given an array and an element x of array as pivot, put x at its correct position in sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear time.
Quicksort works like this.
- An array is divided into subarrays by selecting a pivot element (element selected from the array).While dividing the array, the pivot element should be positioned in such a way that elements less than pivot are kept on the left side and elements greater than pivot are on the right side of the pivot.
- The left and right subarrays are also divided using the same approach. This process continues until each subarray contains a single element.
- At this point, elements are already sorted. Finally, elements are combined to form a sorted array.
An example of quicksort.
Explanation with an example
Consider the following array: 50, 23, 9, 18, 61, 32. We need to sort this array in the most efficient manner without using extra place (inplace sorting).
Step 1:
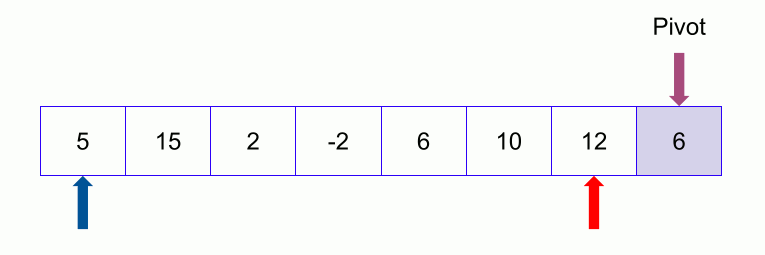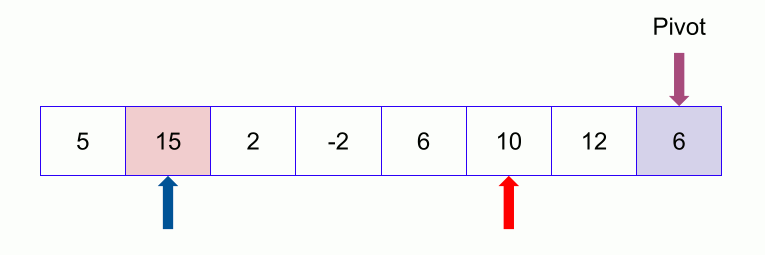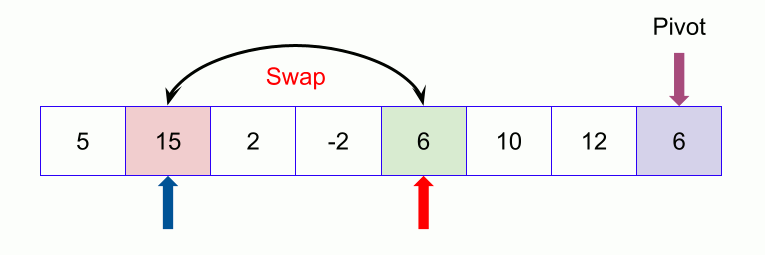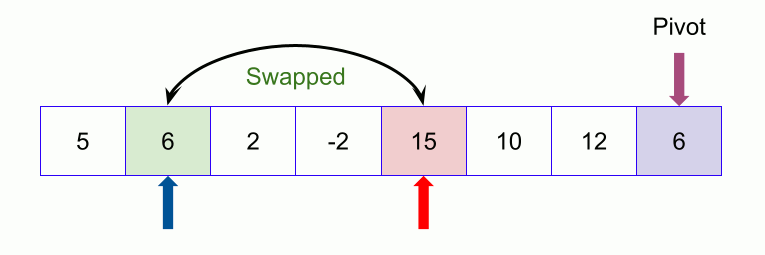
- Make any element as pivot: Decide any value to be the pivot from the list. For convenience of code, we often select the rightmost index as pivot or select any at random and swap with rightmost. Suppose for two values “Low” and “High” corresponding to the first index and last index respectively.
- In our case low is 0 and high is 5.
- Values at low and high are 50 and 32 and value at pivot is 32.
- Partition the array on the basis of pivot: Call for partitioning which rearranges the array in such a way that pivot (32) comes to its actual position (of the sorted array). And to the left of the pivot, the array has all the elements less than it, and to the right greater than it.
- In the partition function, we start from the first element and compare it with the pivot. Since 50 is greater than 32, we don’t make any change and move on to the next element 23.
- Compare again with the pivot. Since 23 is less than 32, we swap 50 and 23. The array becomes
23, 50, 9, 18, 61, 32 - We move on to the next element 9 which is again less than pivot (32) thus swapping it with 50 makes our array as
23, 9, 50, 18, 61, 32. - Similarly, for next element 18 which is less than 32, the array becomes
23, 9, 18, 50, 61, 32. Now 61 is greater than pivot (32), hence no changes. - Lastly, we swap our pivot with 50 so that it comes to the correct position.
Thus the pivot (32) comes at its actual position and all elements to its left are lesser, and all elements to the right are greater than itself.
Step 2: The main array after the first step becomes
23, 9, 18, 32, 61, 50
Step 3: Now the list is divided into two parts:
- Sublist before pivot element
- Sublist after pivot element
Step 4: Repeat the steps for the left and right sublists recursively. The final array thus becomes
9, 18, 23, 32, 50, 61.
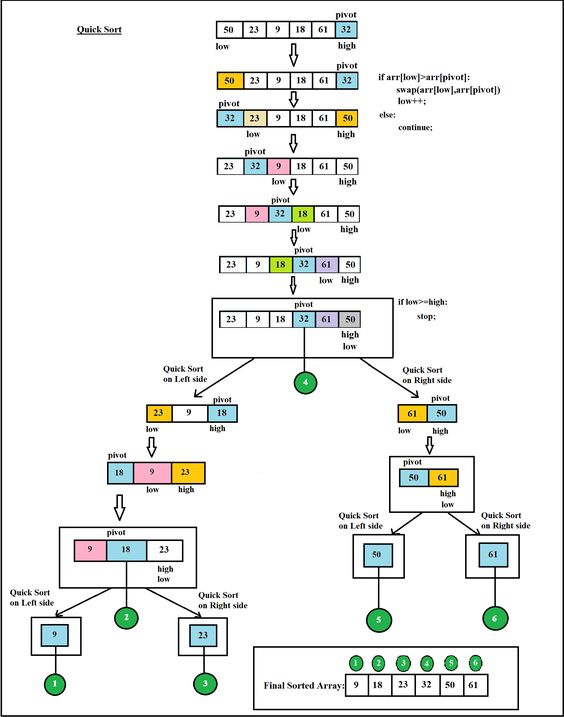
Quicksort Implementation
public int[] sort(int[] array, int low, int high) {
if (low < high) {
// find pivot element such that
// elements smaller than pivot are on the left
// elements greater than pivot are on the right
int pi = partition(array, low, high);
// recursive call on the left of pivot
sort(array, low, pi - 1);
// recursive call on the right of pivot
sort(array, pi + 1, high);
}
return array;
}
// method to find the partition position
int partition(int array[], int low, int high) {
// choose the rightmost element as pivot
int pivot = array[high];
// pointer for greater element
int i = (low - 1);
// traverse through all elements
// compare each element with pivot
for (int j = low; j < high; j++) {
if (array[j] <= pivot) {
// if element smaller than pivot is found
// swap it with the greatr element pointed by i
i++;
// swapping element at i with element at j
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// swapt the pivot element with the greater element specified by i
int temp = array[i + 1];
array[i + 1] = array[high];
array[high] = temp;
// return the position from where partition is done
return (i + 1);
}
Is Quick Sort a stable algorithm?
Quick sort is not a stable algorithm because the swapping of elements is done according to pivot’s position (without considering their original positions). A sorting algorithm is said to be stable if it maintains the relative order of records in the case of equality of keys.
What is Randomised Quick Sort? Why is it used?
-
- Sometimes, it happens that by choosing the rightmost element at all times might result in the worst case scenario.
- In such cases, choosing a random element as your pivot at each step will reduce the probability of triggering the worst case behavior. We will be more likely choosing pivots closer to the center of the array, and when this happens, the recursion branches more evenly and thus the algorithm terminates a lot faster.
- The runtime complexity is expected to be
O(n log n)as the selected random pivots are supposed to avoid the worst case behavior.
Why Quick Sort is better than Merge Sort?
-
- Auxiliary Space : Quick sort is an in-place sorting algorithm whereas Merge sort uses extra space. In-place sorting means no additional storage space is used to perform sorting (except recursion stack). Merge sort requires a new temporary array to merge the sorted arrays thereby making Quick sort the better option.
- Worst Cases : The worst case runtime of quick sort is O(n2) can be avoided by using randomized quicksort as explained in the previous point. Obtaining average case behavior by choosing random pivot element improves the performance and becomes as efficient as merge sort.
- Cache Friendly: Quick Sort is also a cache friendly sorting algorithm as it has good locality of reference when used for arrays.
Which is faster quick sort or merge sort?
Quick sort is faster than the merge sort. Please refer the above question.
Where is quick sort used?
Quick sort is basically used to sort any list in fast and efficient manner. Since the algorithm is inplace, quick sort is used when we have restrictions in space availability too. Please refer to the Application section for further details.
Merge Sort
Trie
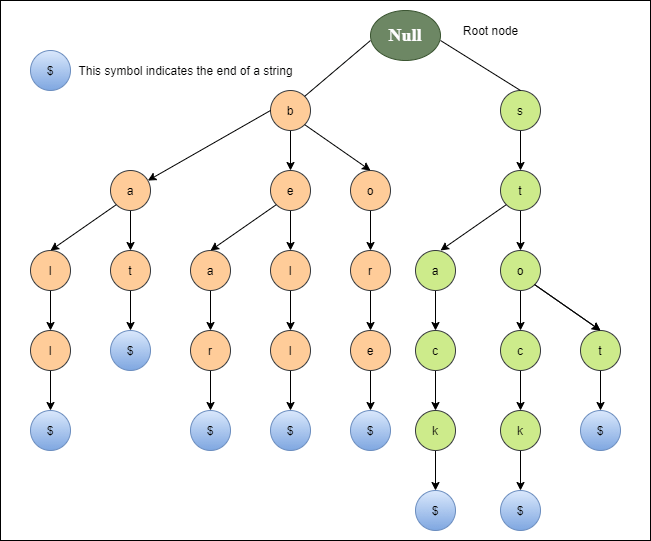
A trie (also known as a digital tree) and sometimes even radix tree or prefix tree (as they can be searched by prefixes), is an ordered tree structure, which takes advantage of the keys that it stores – usually strings. A node’s position in the tree defines the key with which that node is associated, which makes tries different in comparison to binary search trees, in which a node stores a key that corresponds only to that node.
All descendants of a node have a common prefix of a String associated with that node, whereas the root is associated with an empty String.
There may be cases when a trie is a binary search tree, but in general, these are different. Both binary search trees and tries are trees, but each node in binary search trees always has two children, whereas tries’ nodes, on the other hand, can have more.
In a trie, every node (except the root node) stores one character or a digit. By traversing the trie down from the root node to a particular node n, a common prefix of characters or digits can be formed which is shared by other branches of the trie as well.
By traversing up the trie from a leaf node to the root node, a String or a sequence of digits can be formed.