Linked List
Linked List is a very commonly used linear data structure which consists of group of nodes in a sequence. Each node holds its own data and the address of the next node hence forming a chain like structure.
Linked Lists are used to create trees and graphs.
Advantages of Linked List
- Linkedlist is dynamic in nature which means it can expand in constant time. It does not have to create a new array as dynamic array does.
- Insertion and deletion operations can be easily implemented.
- Stacks and queues can be easily executed.
- Linked List reduces the access time.
Disadvantages of Linked List
- The memory is wasted as pointers require extra memory for storage.
- No element can be accessed randomly; it has to access each node sequentially.
- Reverse Traversing is difficult in linked list.
Where to use Linked List
- Linked lists are used to implement stacks, queues, graphs, etc.
- Linked lists let you insert elements at the beginning and end of the list.
- In Linked Lists we don’t need to know the size in advance.
When to use Linked List
- When you insert and delete elements often from a list.
There are 3 different implementations of Linked List available, they are:
- Singly Linked List
- Doubly Linked List
- Circular Linked List
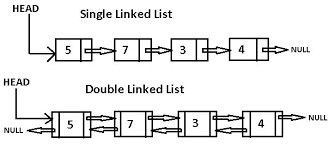
Singly Linked List
Singly linked lists contain nodes which have a data part as well as an address part i.e. next, which points to the next node in the sequence of nodes.
The operations we can perform on singly linked lists are insertion, deletion and traversal.
@ToString
@NoArgsConstructor
@AllArgsConstructor
@Data
public class Customer {
private String firstName;
private String lastName;
private String email;
}
@ToString
@Data
public class SingleNode {
private Customer data;
private SingleNode next;
public SingleNode(Customer data) {
this(data, null);
}
public SingleNode(Customer data, SingleNode next) {
this.data = data;
this.next = next;
}
}
@NoArgsConstructor
@Data
public class MySingleLinkedList {
int size = 0;
private SingleNode head;
private SingleNode tail;
public MySingleLinkedList(SingleNode head) {
append(head);
}
/**
* add to end of list<br>
* 1. If the Linked List is empty then we simply, add the new Node as the Head of the Linked List.<br>
* 2. If the Linked List is not empty then we find the last node, and make it' next to the new Node, hence making
* the new node the last Node.
*
* Time complexity of append is O(n) where n is the number of nodes in the linked list. Since there is a loop from
* head to end, the function does O(n) work. This method can also be optimized to work in O(1) by keeping an extra
* pointer to the tail of the linked list.
*/
public void append(SingleNode node) {
if (node == null) {
return;
}
if (this.head == null) {
this.head = node;
this.tail = node;
} else {
this.tail.setNext(node);
this.tail = node;
}
size++;
}
/**
* append to front of list<br>
* 1. The first Node is the Head for any Linked List.<br>
* 2. When a new Linked List is instantiated, it just has the Head, which is Null.<br>
* 3. Else, the Head holds the pointer to the first Node of the List.<br>
* 4. When we want to add any Node at the front, we must make the head point to it.<br>
* 5. And the Next pointer of the newly added Node, must point to the previous Head, whether it be NULL(in case of
* new List) or the pointer to the first Node of the List.<br>
* 6. The previous Head Node is now the second Node of Linked List, because the new Node is added at the front.<br>
*/
public void prepend(SingleNode node) {
if (node == null) {
return;
}
if (this.head == null) {
this.head = node;
} else {
node.setNext(this.head);
this.head = node;
}
size++;
}
/**
* add at position of list
*/
public void add(int index, SingleNode node) {
if (node == null) {
return;
}
int count = 0;
SingleNode currentNode = this.head;
if (this.head.equals(currentNode)) {
/*
* adding to the head
*/
node.setNext(currentNode);
this.head = node;
} else if (this.tail.equals(currentNode)) {
this.tail.setNext(node);
this.tail = node;
}
SingleNode previous = null;
while (currentNode.getNext() != null) {
if (index == count) {
break;
}
previous = currentNode;
currentNode = currentNode.getNext();
count++;
}
node.setNext(currentNode);
previous.setNext(node);
size++;
}
/**
* is empty?
*/
public boolean isEmpty() {
return size <= 0 || this.head == null;
}
/**
* exist? search by email
*/
public boolean existByEmail(String email) {
if (email == null || email.length() <= 0) {
return false;
}
if (this.head == null) {
return false;
} else {
SingleNode currentNode = this.head;
/**
* if email not found, keep checking the next node<br>
* when email is found, break out of while loop
*/
while (!currentNode.getData().getEmail().equalsIgnoreCase(email.toLowerCase())) {
/**
* next is null, so email is not found
*/
if (currentNode.getNext() == null) {
return false;
}
currentNode = currentNode.getNext();
}
return true;
}
}
/**
* get node on index
*/
public SingleNode get(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("index out of bounds");
}
if (index == 0) {
return this.head;
} else if (index == (size - 1)) {
return this.tail;
} else {
int count = 0;
SingleNode currentNode = this.head;
while (currentNode.getNext() != null) {
currentNode = currentNode.getNext();
count++;
if (index == count) {
break;
}
}
return currentNode;
}
}
/**
* remove node base on index<br>
* 1. If the Node to be deleted is the first node, then simply set the Next pointer of the Head to point to the next
* element from the Node to be deleted.<br>
* 2. If the Node is in the middle somewhere, then find the Node before it, and make the Node before it point to the
* Node next to it.<br>
*/
public void removeAt(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("index out of bounds");
}
if (index==0) {
this.head = this.head.getNext();
return;
}
int count = 1;
SingleNode previous = this.head;
SingleNode currentNode = this.head.getNext();
SingleNode next = null;
while (count < index) {
previous = currentNode;
currentNode = currentNode.getNext();
next = currentNode.getNext();
count++;
}
if (currentNode.equals(this.tail)) {
this.tail = previous;
this.tail.setNext(null);
} else {
// drop currentNode
previous.setNext(next);
}
}
/**
* remove all<br>
* set head to null
*/
public void removeAll() {
this.head = null;
this.tail = null;
}
/**
* print out list
*/
public void printList() {
if (this.head == null) {
System.out.println("list is empty");
}
int count = 0;
SingleNode node = this.head;
while (node != null) {
System.out.println("index: " + count);
System.out.println("data: " + node.getData().toString());
node = node.getNext();
if (node == null) {
System.out.println("tail: " + tail.getData().toString());
System.out.println("end of list\n");
}
System.out.println("\n");
count++;
}
}
}
Doubly Linked List
In a doubly linked list, each node contains a data part and two addresses, one for the previous node and one for the next node.
@AllArgsConstructor
@ToString
@Data
public class DoubleNode {
private DoubleNode prev;
private Customer data;
private DoubleNode next;
public DoubleNode(Customer data) {
this(null, data, null);
}
}
@NoArgsConstructor
@Data
public class MyDoubleLinkedList {
int size = 0;
private DoubleNode head;
private DoubleNode tail;
public MyDoubleLinkedList(DoubleNode head) {
append(head);
}
/**
* add to end of list<br>
* 1. If the Linked List is empty then we simply, add the new Node as the Head of the Linked List.<br>
* 2. If the Linked List is not empty then we find the last node, and make it' next to the new Node, hence making
* the new node the last Node.
*/
public void append(DoubleNode node) {
if (node == null) {
return;
}
if (this.head == null) {
this.head = node;
this.tail = node;
} else {
DoubleNode currentNode = this.head;
while (currentNode.getNext() != null) {
currentNode = currentNode.getNext();
}
// order doesn't matter, as long as the last operation is tail=node
this.tail.setNext(node);
node.setPrev(this.tail);
this.tail = node;
}
size++;
}
/**
* append to front of list<br>
* 1. The first Node is the Head for any Linked List.<br>
* 2. When a new Linked List is instantiated, it just has the Head, which is Null.<br>
* 3. Else, the Head holds the pointer to the first Node of the List.<br>
* 4. When we want to add any Node at the front, we must make the head point to it.<br>
* 5. And the Next pointer of the newly added Node, must point to the previous Head, whether it be NULL(in case of
* new List) or the pointer to the first Node of the List.<br>
* 6. The previous Head Node is now the second Node of Linked List, because the new Node is added at the front.<br>
*/
public void prepend(DoubleNode node) {
if (node == null) {
return;
}
if (this.head == null) {
this.head = node;
} else {
// order doesn't matter, as long as the last operation is head=node
this.head.setPrev(node);
node.setNext(this.head);
this.head = node;
}
size++;
}
/**
* add at position of list
*/
public void add(int index, DoubleNode node) {
if (node == null) {
return;
}
int count = 0;
DoubleNode currentNode = this.head;
if (index == 0) {
node.setNext(currentNode);
this.head = node;
} else if (index == (size - 1)) {
this.tail.setNext(node);
this.tail = node;
} else {
DoubleNode previous = null;
while (currentNode.getNext() != null) {
if (index == count) {
break;
}
previous = currentNode;
currentNode = currentNode.getNext();
count++;
}
node.setNext(currentNode);
previous.setNext(node);
}
size++;
}
/**
* is empty?
*/
public boolean isEmpty() {
return size <= 0 || this.head == null;
}
/**
* exist? search by email
*/
public boolean existByEmail(String email) {
if (email == null || email.length() <= 0) {
return false;
}
if (this.head == null) {
return false;
} else {
DoubleNode currentNode = this.head;
/**
* if email not found, keep checking the next node<br>
* when email is found, break out of while loop
*/
while (!currentNode.getData().getEmail().equalsIgnoreCase(email.toLowerCase())) {
/**
* next is null, so email is not found
*/
if (currentNode.getNext() == null) {
return false;
}
currentNode = currentNode.getNext();
}
return true;
}
}
/**
* get node on index
*/
public DoubleNode get(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("index out of bounds");
}
if (index == 0) {
return this.head;
}
if (index == 0) {
return this.head;
} else if (index == (size - 1)) {
return this.tail;
} else {
int count = 0;
DoubleNode currentNode = this.head;
while (currentNode.getNext() != null) {
currentNode = currentNode.getNext();
count++;
if (index == count) {
break;
}
}
return currentNode;
}
}
/**
* remove node base on index<br>
* 1. If the Node to be deleted is the first node, then simply set the Next pointer of the Head to point to the next
* element from the Node to be deleted.<br>
* 2. If the Node is in the middle somewhere, then find the Node before it, and make the Node before it point to the
* Node next to it.<br>
*/
public void remove(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("index out of bounds");
}
int count = 0;
if (index == 0) {
this.head = this.head.getNext();
this.head.setPrev(null);
} else if (index == (size - 1)) {
this.tail = this.tail.getPrev();
this.tail.setNext(null);
} else {
DoubleNode previous = null;
DoubleNode currentNode = this.head;
DoubleNode next = null;
while (currentNode.getNext() != null) {
if (index == count) {
break;
}
previous = currentNode;
currentNode = currentNode.getNext();
next = currentNode.getNext();
count++;
}
previous.setNext(next);
next.setPrev(previous);
}
}
/**
* remove all<br>
* set head to null
*/
public void removeAll() {
this.head = null;
this.tail = null;
}
/**
* print out list
*/
public void printList() {
if (this.head == null) {
System.out.println("list is empty");
}
int count = 0;
DoubleNode node = this.head;
while (node != null) {
System.out.println("index: " + count);
System.out.println("prev: " + ((node.getPrev() != null) ? node.getPrev().getData().toString() : ""));
System.out.println("current: " + node.getData().toString());
System.out.println("next: " + ((node.getNext() != null) ? node.getNext().getData().toString() : ""));
node = node.getNext();
if (node == null) {
System.out.println("tail: " + tail.getData().toString());
System.out.println("end of list\n");
}
System.out.println("\n");
count++;
}
}
}
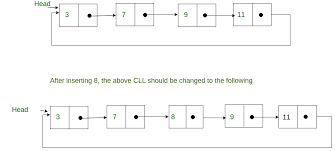
Circular Linked List
In circular linked list the last node of the list holds the address of the first node hence forming a circular chain.
Time Complexity
| Data Structure | Time Complexity | Space Complexity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Average | Worst | Worst | |||||||
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion | ||
| Singly-Linked List | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Doubly-Linked List | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
- add() – appends an element to the end of the list. So it only updates the tail node, therefore O(1) constant-time complexity.
- add(index, element) – in average runs in O(n) time
- get() – searching for an element takes O(n) time
- remove(element) – to remove an element, only pointers have to be updated. This operation is O(1).
- remove(index) – to remove an element by index, we first need to find it, therefor the overall complexity is O(n)
- contains() – also has O(n) time complexity
Multithreading
–
Divide and Conquer
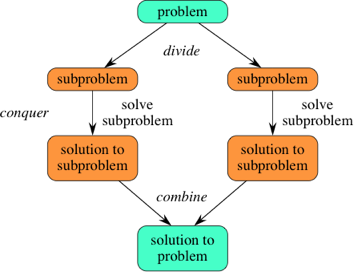
Divide and Conquer is a very popular algorithm that many people use to solve problems. With Divide and Conquer, a problem in hand, is divided into smaller sub-problems and then each problem is solved independently. When we keep on dividing the subproblems into even smaller sub-problems, we may eventually reach a stage where no more division is possible. Those smallest sub-problem are solved. The solution of all sub-problems is finally merged in order to obtain the solution of the original problem.
Keep in mind that the divide and conquer algorithm is founded on recursion. It involves understanding a problem, separating it into subproblems, and combining the solutions to solve the larger problem just like recursion.
Divide and Conquer Strategy
- Divide – breaking the problem into smaller sub-problems of the same problem
- Conquer – solve the problem if it’s small enough(base case). If the problem is still not small enough, divide it and recursively solve its sub-problems. This step receives a lot of smaller sub-problems to be solved. Generally, at this level, the problems are considered ‘solved’ on their own.
- Combine – combine solutions from sub problems to generate the solution for the original problem.
/**
* Recursion used for factorial<br>
* Start from the top and go to bottom, then calculation will start from bottom back to top
*/
private static int factorial(int num) {
/**
* validation
*/
if (num < 0) {
throw new IllegalArgumentException("num is invalid");
}
/**
* base case, solve problem when it's small enough
*/
if (num == 0) {
return 1;
}
/**
* recursive case, divide into sub-problems
*/
return num * factorial(num - 1);
}
A problem can be also like this.
What are the disadvantages of Divide and Conquer?
Divide and Conquer algorithm requires recursion, which takes up more space than other processes. Your recursion stacks may overflow, causing the solution to fail.
Choosing base cases may also pose problems. Small, simple base cases typically lead to easier problems and solutions, while large base cases usually improve efficiency.
What are the advantages of Divide and Conquer?
Divide and Conquer algorithm helps solve complex problems relatively quickly and with much less effort(lines of code). It works well with processors because of their parallel structure. It also allows for easy storing and accessing by memory caches.
Where is Divide and Conquer being used?
Divide and Conquer is being used in these algorithms:
- Merge Sort
- Quick Sort
- Binary Search
This method usually allows us to reduce the time complexity by a large extent.
For example, Bubble Sort uses a complexity of O(n^2), whereas quicksort (an application Of Divide And Conquer) reduces the time complexity to O(nlog(n)). Linear Search has time complexity O(n), whereas Binary Search (an application Of Divide And Conquer) reduces time complexity to O(log(n)).
When do you use Divide and Conquer?
Divide and Conquer should be used when same subproblems are not evaluated many times.
For example, Binary Search is a Divide and Conquer algorithm, we never evaluate the same subproblems again.
Here is an article that really caught my attention. It talks about how to use Divide and Conquer in business.
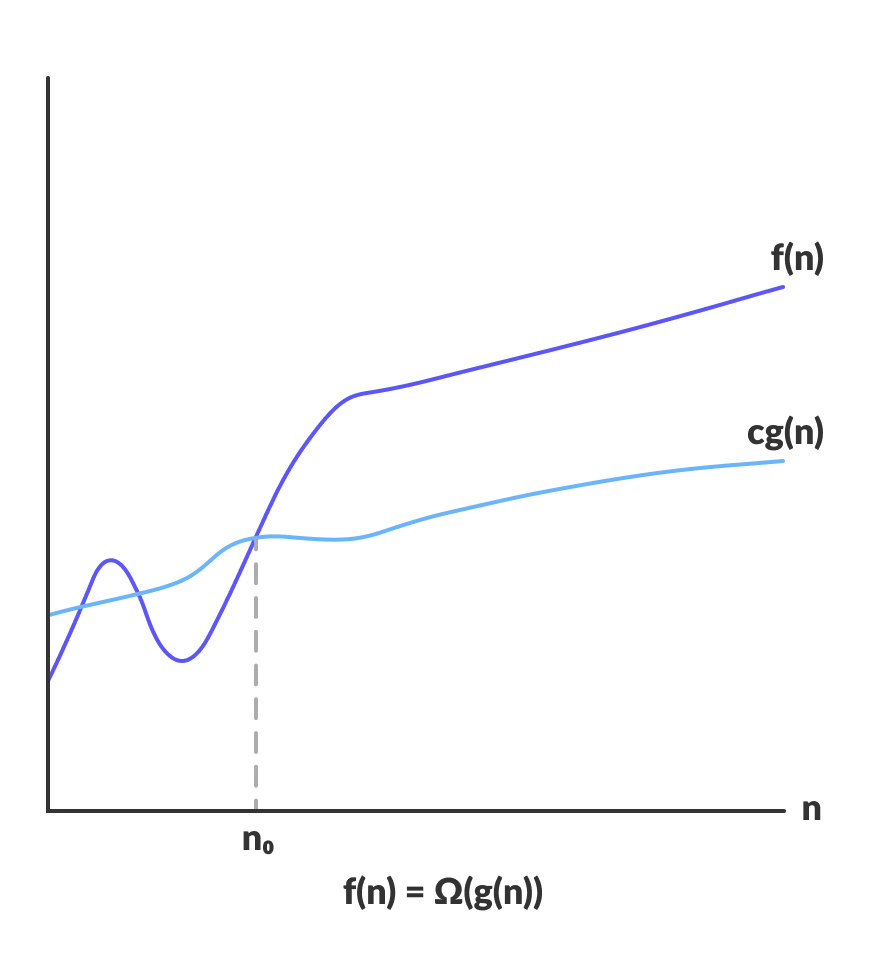
Big Omega Notation
The Omega notation represents the lower bound of the running time of an algorithm. It provides the best case complexity of an algorithm.
So if we represent a complexity of an algorithm in Omega notation, it means that the algorithm cannot be completed in less time than this, it would at least take the time represented by Omega notation or it can take more (when not in best case scenario).
For example:
f(n) = 3n + 2
g(n) = n
If we want to represent f(n) as Ω(g(n)) then it must satisfy f(n) >= C g(n) for all values of C > 0 and n0>= 1
f(n) >= C g(n)
⇒3n + 2 >= C n
Above condition is always TRUE for all values of C = 1 and n >= 1.
By using Big – Omega notation we can represent the time complexity as follows.
3n + 2 = Ω(n)
Algorithm interview – Big O
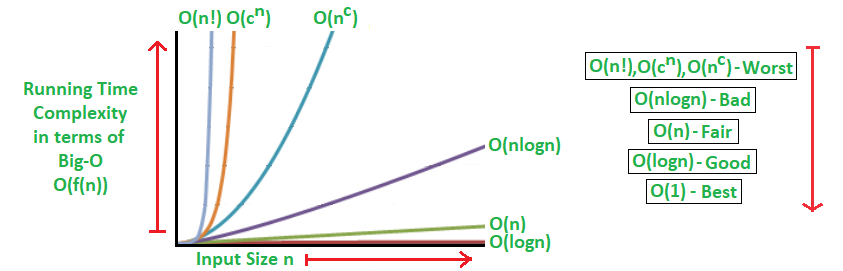
Big O is about how long an algorithm takes to run from start to end and how well it scales based on the size of the input or dataset.
Big O is mostly measured based on the worst-case scenario even though some algorithms might finish early based on some logic.
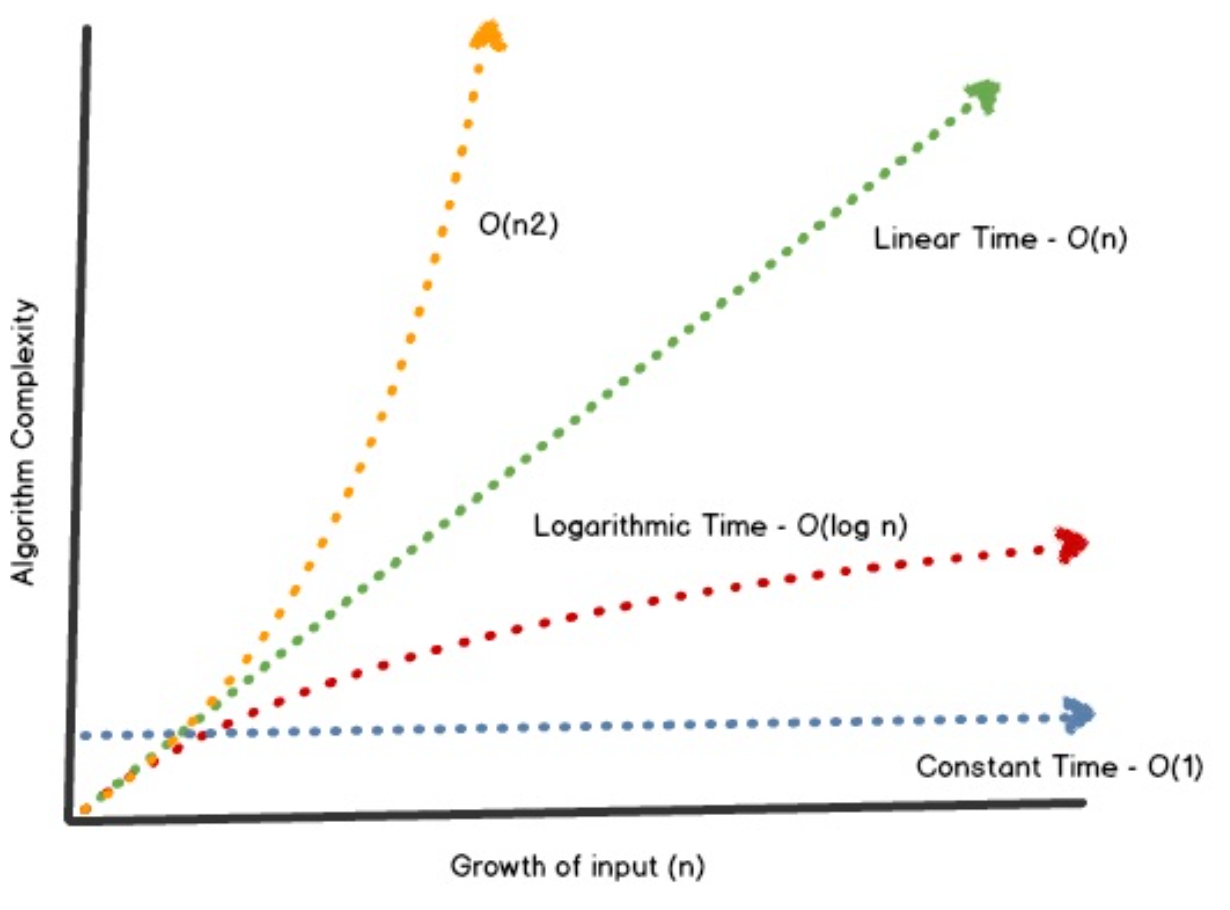
Here is another graph for more clarity.
O(1) – constant time
This runtime is said to be fixed or constant. It does not matter how big the input or dataset is, the algorithm takes the same amount of time to run. This means that the size of the dataset is irrelevant, the algorithm will always take a constant time. 1 item takes 1 second, 10 items take 1 second, 100 items take 1 second. It always takes the same amount of time.
public int getFirstItem(int[] items) {
return items[0];
}
This function above takes an int array (items). But regardless of the size of the input array, it will always take one step to run(return the first item)

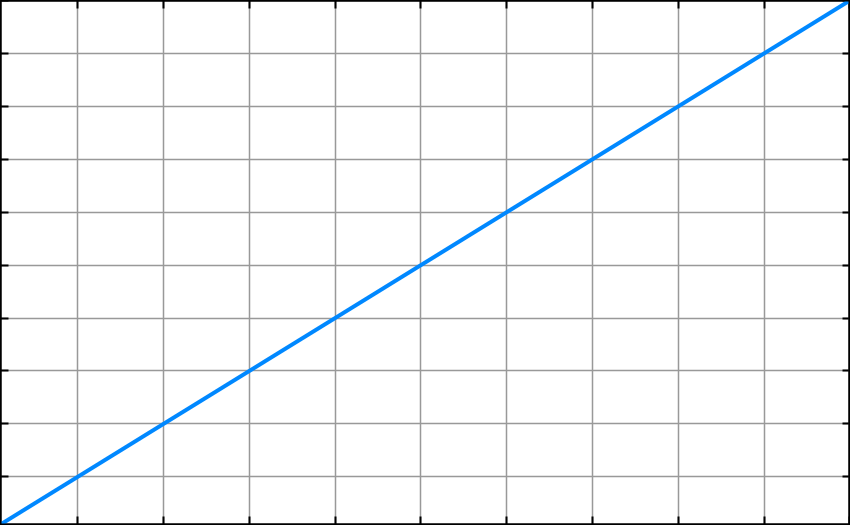
O(n) – n time or linear time
This runtime is said to be n time or linear time. As the size of the input or dataset increases the algorithm processing time increases at the same rate.
public void sendWelcomeNoteToUsers(User[] users) {
for (User user : users) {
emailService.sendNote(user);
...
}
}
As the size of the array of users increases, the sendWelcomeNoteToUsers method runtime increases. Dataset and time taken grow proportionately. 1 item takes 1 second, 10 items take 10 seconds, 100 items take 100 seconds.
Sometimes you might see something like this and think differently.
public User getUserByEmail(User[] users, String email){
for (int i = 0; i < users.length; i++) {
if (users[i].equals(email)) {
return users[i];
}
}
}
Even though the getUserByEmail method might find a user early and not get to the end of the array. Big O is based on the worst-case scenario of an algorithm so it is still O(n).
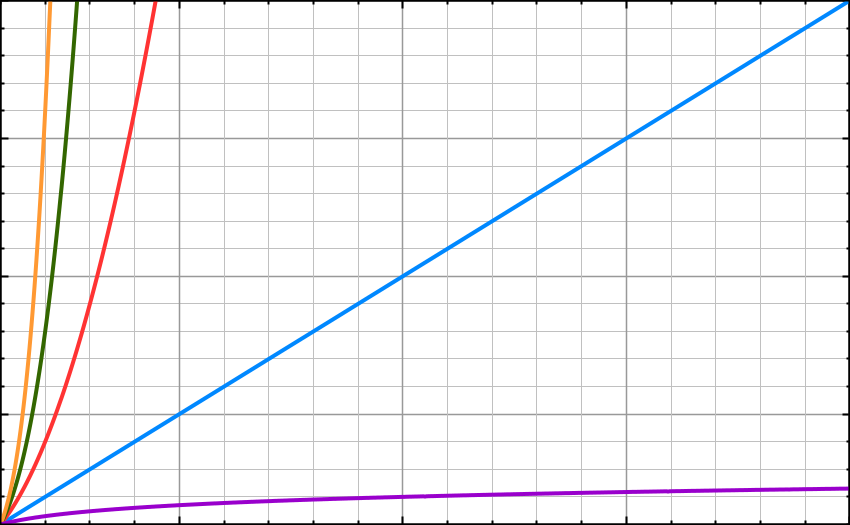
O(N²) – n square or quadratic time
The Quadratic time or n square time increases at twice the rate of O(n).
public static void suspendAllUsersWithinPlans(Plan[] plans) {
for (Plan plan : plans) {
List<User> users = plan.getUsers();
for (User user : users) {
// suspend logic goes here.
}
}
}
This runtime is extra slow. 1 item takes 1 second, 10 items take 100, 100 items take 10000. The outer loop runs n times and the inner loop runs n times for each iteration of the outer loop, giving us n².
Bubble sort is an example of quadratic time complexity.

private static void bubble_sort(int[] input, boolean ascending) {
int inputLength = input.length;
int temp;
boolean is_sorted;
for (int i = 0; i < inputLength; i++) {
is_sorted = true;
for (int j = 1; j < (inputLength - i); j++) {
if (ascending) {
if (input[j - 1] > input[j]) {
temp = input[j - 1];
input[j - 1] = input[j];
input[j] = temp;
is_sorted = false;
}
} else {
if (input[j - 1] < input[j]) {
temp = input[j - 1];
input[j - 1] = input[j];
input[j] = temp;
is_sorted = false;
}
}
}
// is sorted? then break it, avoid useless loop.
if (is_sorted) break;
}
}
As you can see, bubble sort has two for loops. An outer loop and an inner loop.

O(log n) – log n time
The log n time is the opposite of n². Logarithm is the opposite of exponential. Exponential grows by being multiplied and logarithm grows(gettings smaller) by being divided. Log n is the case when a set of data is repeatedly divided into half and the middle element is processed. This means that for one iteration of the algorithm, technically speaking, two items are processed.
O(log n) is not as good as constant, but still pretty good. Log n increases with the size of the data set, but not proportionately. This means the algorithm takes longer per item on smaller datasets relative to larger ones. 1 item takes 1 second, 10 items take 2 seconds, 100 items take 3 seconds. If your dataset has 10 items, each item causes 0.2 seconds latency. If your dataset has 100, it only takes 0.03 seconds extra per item. This makes log n algorithms very scalable.
Binary Search(sorted dataset) is the primary example of the log n.
public static int binarySearch(int[] elements, int target) {
int left = 0;
int right = elements.length - 1;
while (left <= right)
{
int middle = (left + right) / 2;
if (target < elements[middle])
{
right = middle - 1;
}
else if (target > elements[middle])
{
left = middle + 1;
}
else {
return middle;
}
}
return -1;
}
public static void main(String[] args){
int[] arr1 = {-20, 3, 15, 81, 432};
// test when the target is in the middle
int index = binarySearch(arr1,15);
System.out.println(index);
// test when the target is the first item in the array
index = binarySearch(arr1,-20);
System.out.println(index);
// test when the target is in the array - last
index = binarySearch(arr1,432);
System.out.println(index);
// test when the target is not in the array
index = binarySearch(arr1,53);
System.out.println(index);
}

O(n log n) – n log n
This runtime is the case when a set of data is repeatedly divided into half and each half is processed again independently.
for (int i = 1; i <= n; i++){
for(int j = 1; j < 8; j = j * 2) {
System.out.println("Hey - I'm busy looking at: " + i + " and " + j);
}
}

O(2^n) – exponential growth
This runtime grows exponentially. Adding one element to the input dramatically increases the processing time.
For example. Let’s say you are to find combinations; if you have a list of 150 people and you would like to find every combination of groupings; everyone by themselves, all of the groups of 2 people, all of the groups of 3 people, etc. Using a simple program which takes each person and loops through the combinations, if I add one extra person then it’s going to increase the processing time exponentially. Every new element will double the processing time.
O(kn) algorithms will get k times bigger with every additional input. O(2n) algorithms double it’s processing time with every additional input. O(3n) algorithms triple it’s processing time with every additional input.
int k = 5;
int n = 6;
int power = (int)Math.pow(k, n);
System.out.println("power: " + power);
for (int i = 1; i <= power; i++){
System.out.println("Hey - I'm busy looking at: " + i);
}
O(n!) – factorial time
In most cases, this is the worst runtime. This class of algorithms has a run time proportional to the factorial of the input size.
for (int i = 1; i <= factorial(n); i++) {
System.out.println("Hey - I'm busy looking at: " + i);
}
....
public int factorial(int number) {
int fact = 1;
for (int i = 1; i <= number; i++) {
fact = fact * i;
}
return fact;
}


Space Complexity
Space complexity is the space used by the input values plus auxiliary space which is the extra space or the temporary space used by the algorithm during its execution.
Space complexity = auxiliary space + input space
public static int getLargestItem(int[] items) {
int largest = Integer.MIN_VALUE;
for (int item : items) {
if (item > largest) {
largest = item;
}
}
return largest;
}
The variable largest takes some space to hold the int min value.
Similar to Time Complexity, Space complexity also plays a crucial role in determining the efficiency of an algorithm/program. If an algorithm takes up a lot of time, you can still wait, run/execute it to get the desired output. But, if a program takes up a lot of memory space, the compiler will not let you run it.