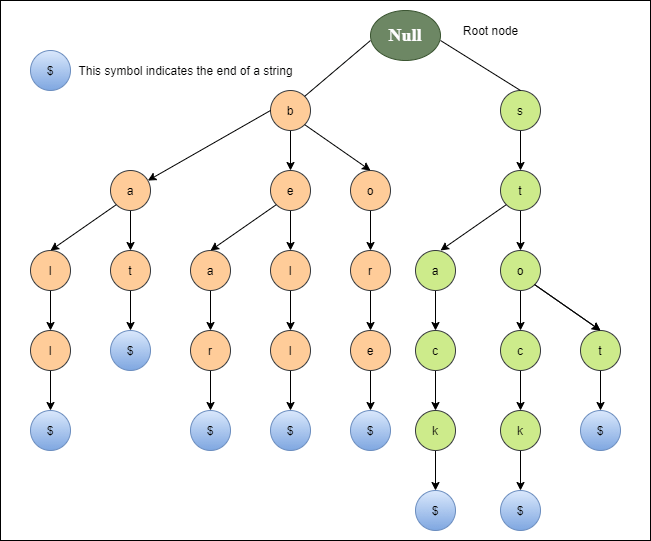
Trie
A trie (also known as a digital tree) and sometimes even radix tree or prefix tree (as they can be searched by prefixes), is an ordered tree structure, which takes advantage of the keys that it stores – usually strings. A node’s position in the tree defines the key with which that node is associated, which makes tries different in comparison to binary search trees, in which a node stores a key that corresponds only to that node.
All descendants of a node have a common prefix of a String associated with that node, whereas the root is associated with an empty String.
There may be cases when a trie is a binary search tree, but in general, these are different. Both binary search trees and tries are trees, but each node in binary search trees always has two children, whereas tries’ nodes, on the other hand, can have more.
In a trie, every node (except the root node) stores one character or a digit. By traversing the trie down from the root node to a particular node n, a common prefix of characters or digits can be formed which is shared by other branches of the trie as well.
By traversing up the trie from a leaf node to the root node, a String or a sequence of digits can be formed.