Binary Search is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. It works only on a sorted set of elements. To use binary search on a collection, the collection must first be sorted.

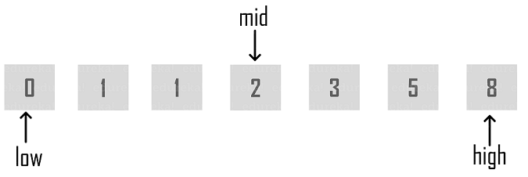
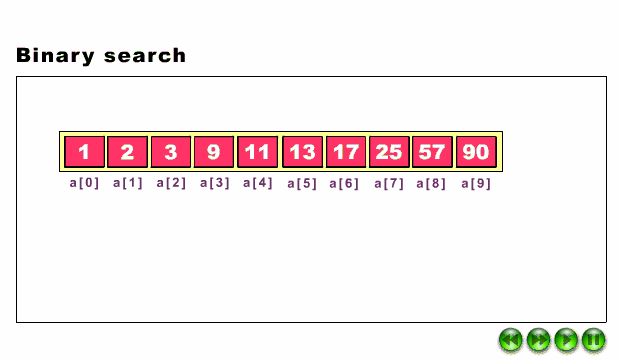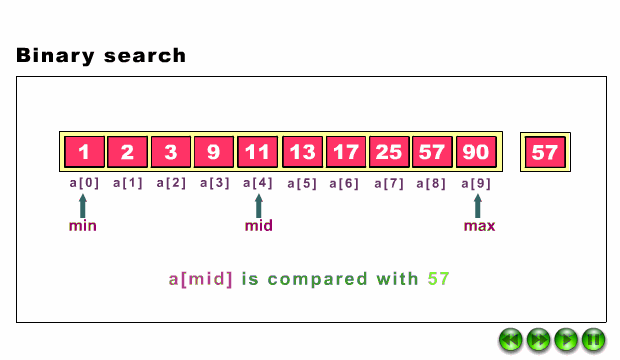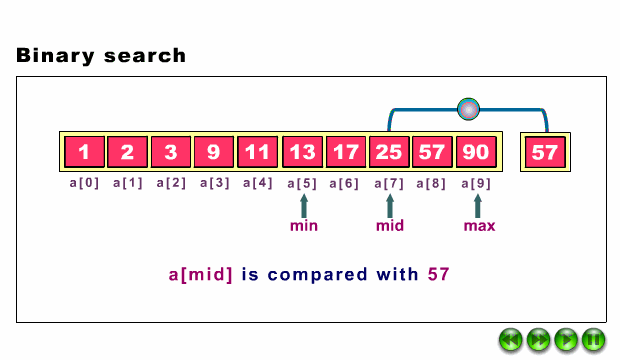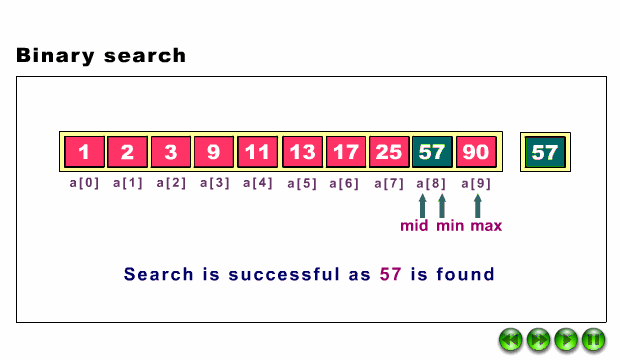
When the binary search is used to perform operations on a sorted set, the number of iterations can always be reduced on the basis of the value that is being searched. You can see in the below snapshot of finding the mid element. The analogy of binary search is to use the information that the array is sorted and reduce the time complexity to O(log n).

Advantages

• A binary search algorithm is a fairly simple search algorithm to implement. 

• It is a significant improvement over linear search and performs almost the same in comparison to some of the harder to implement search algorithms.
• The binary search algorithm breaks the list down in half on every iteration, rather than sequentially combing through the list. On large lists, this method can be really useful.

Note that the array has to be sorted.

Binary Search in a iterative way

Time: O(log n)
Space: O(log n) or O(1)

public int search(int array[], int searchElement, int lowIndex, int highIndex) {

    // Repeat until the pointers low and high meet each other
    while (lowIndex <= highIndex) {

        // get index of mid element
        int midIndex = lowIndex + (highIndex - lowIndex) / 2;

        int midValue = array[midIndex];

        // if element to be searched is the mid element
        if (midValue == searchElement) {
            return midIndex;
        }

        // if element is less than mid element
        // search only the left side of mid
        if (midValue < searchElement) {
            lowIndex = midIndex + 1;

            // if element is greater than mid element
            // search only the right side of mid
        } else {
            highIndex = midIndex - 1;
        }
    }

    return -1;
}

Notice how the middle index is generated (int mid = low + ((high – low) / 2). This to accommodate for extremely large arrays. If the middle index is generated simply by getting the middle index (int mid = (low + high) / 2), an overflow may occur for an array containing 2³⁰ or more elements as the sum of low + high could easily exceed the maximum positive int value.

Binary Search in a recursive way
Time: O(log n)
Space: O(log n)

public int search(int array[], int searchElement, int lowIndex, int highIndex) {
    if (highIndex >= lowIndex) {
        int midIndex = lowIndex + (highIndex - lowIndex) / 2;

        int midValue = array[midIndex];

        // check if mid element is searched element
        if (midValue == searchElement) {
            return midIndex;
        }

        // Search the left half of mid
        if (midValue > searchElement) {
            return searchWithRecursion(array, searchElement, lowIndex, midIndex - 1);
        }

        // Search the right half of mid
        return searchWithRecursion(array, searchElement, midIndex + 1, highIndex);
    }

    return -1;
}

Tests

CustomBinarySearch bs = new CustomBinarySearch();

int[] numbers = {1, 4, 6, 45, 367};

Arrays.sort(numbers);

int searchNumber = 6;

int searchNumberIndex = bs.search(numbers, searchNumber, 0, numbers.length - 1);

System.out.println("searchNumber: " + searchNumber + ", searchNumberIndex: " + searchNumberIndex);

searchNumberIndex = bs.searchWithRecursion(numbers, searchNumber, 0, numbers.length - 1);

System.out.println("searchNumber: " + searchNumber + ", searchNumberIndex: " + searchNumberIndex);

Is it better to do a recursive binary search or an iterative binary search?

int index = Arrays.binarySearch(sortedArray, key);

int index = Collections.binarySearch(sortedList, key);

Source code on Github